DeepSeekMath: Pushing the Limits of Mathematical Reasoning in Open Language Models
by DeepSeek AI
TL;DR
이 연구를 시작하게 된 배경과 동기는 무엇입니까?
수학적 추론은 복잡하고 구조화된 특성으로 인해 언어 모델에게 상당한 도전 과제를 제시합니다. 현재 GPT-4와 Gemini-Ultra와 같은 최첨단 모델들은 수학적 추론에서 뛰어난 성능을 보이지만 공개적으로 사용할 수 없으며, 접근 가능한 오픈소스 모델들은 성능 면에서 크게 뒤처져 있습니다. 이러한 격차를 해소하기 위해 연구팀은 오픈소스 모델의 수학적 능력을 크게 향상시키고 학술 벤치마크에서 GPT-4의 성능 수준에 근접하는 도메인 특화 언어 모델을 개발하고자 했습니다. 특히 대규모 매개변수 수에 의존하지 않고도 효율적인 데이터 선택과 학습 방법을 통해 강력한 수학적 추론 능력을 갖춘 모델을 구축하는 것이 목표였습니다.
이 연구에서 제시하는 새로운 해결 방법은 무엇입니까?
이 연구는 두 가지 핵심적인 혁신을 제시합니다.
첫째, 세심하게 설계된 데이터 선택 파이프라인을 통해 Common Crawl에서 1,200억 개의 고품질 수학 토큰으로 구성된 DeepSeekMath Corpus를 구축했습니다. 이 파이프라인은 fastText 기반 분류기를 사용하여 수학적 콘텐츠를 식별하고, 반복적인 과정을 통해 데이터의 품질과 다양성을 향상시켰습니다. 이는 기존 수학 코퍼스보다 7-9배 더 큰 규모입니다.
둘째, 근접 정책 최적화(PPO)의 변형인 그룹 상대 정책 최적화(GRPO)를 도입했습니다. GRPO는 비평 모델을 사용하지 않고 대신 그룹 점수에서 기준선을 추정하여 PPO에 비해 메모리 사용량을 크게 줄이면서도 수학적 추론 능력을 효과적으로 향상시킵니다. 또한 RFT, DPO, PPO, GRPO와 같은 다양한 학습 방법을 이해하기 위한 통합 패러다임을 제공합니다.
제안된 방법은 어떻게 구현되었습니까?
DeepSeekMath는 DeepSeek-Coder-Base-v1.5 7B를 기반으로 구현되었으며, 500B 토큰에 대해 추가 학습을 진행했습니다. 학습 데이터는 DeepSeekMath 코퍼스(56%), AlgebraicStack(4%), arXiv(10%), Github 코드(20%), 그리고 일반 자연어 데이터(10%)로 구성되었습니다.
데이터 수집 파이프라인은 네 번의 반복을 통해 35.5M개의 수학적 웹 페이지를 수집하여 120B 토큰을 확보했습니다. 벤치마크 오염을 방지하기 위해 GSM8K, MATH 등의 평가 데이터셋과 일치하는 콘텐츠를 필터링했습니다.
학습 과정은 세 단계로 진행되었습니다.
- 사전 학습: DeepSeekMath-Base 7B 모델 구축
- 지도 학습 미세 조정: 776K개의 수학적 명령어 튜닝 데이터로 DeepSeekMath-Instruct 7B 개발
- 강화 학습: GRPO를 적용하여 DeepSeekMath-RL 7B 개발
GRPO 구현에서는 각 질문에 대해 64개의 출력을 샘플링하고, 그룹 내 출력의 상대적 보상을 기반으로 어드밴티지를 계산했습니다. 학습률은 1e-6, KL 계수는 0.04로 설정되었습니다.
이 연구의 결과가 가지는 의미는 무엇입니까?
DeepSeekMath-RL 7B는 경쟁 수준의 MATH 벤치마크에서 51.7%의 정확도를 달성했으며, 자기 일관성(self-consistency)을 적용하면 60.9%까지 향상됩니다. 이는 오픈소스 커뮤니티에서 처음으로 50%를 넘는 성과로, 7B부터 70B까지의 모든 오픈소스 모델과 대부분의 비공개 모델을 능가하며 GPT-4와 Gemini-Ultra의 성능에 근접합니다.
이 연구는 대규모 모델 크기만으로는 수학적 추론 능력을 향상시키기에 충분하지 않으며, 고품질 데이터와 효과적인 학습 방법론의 조합이 중요하다는 것을 보여줍니다. 특히 코드 학습이 수학적 추론 능력 향상에 도움이 된다는 것을 실험적으로 입증했으며, 이는 “코드 학습이 추론 능력을 향상시키는가?”라는 오랜 질문에 부분적인 답변을 제공합니다.
또한 강화 학습이 명령어 튜닝 모델의 성능을 향상시키는 메커니즘에 대한 통찰을 제공하며, RL이 모델의 출력 분포를 더 견고하게 만들어 전반적인 성능을 향상시킨다는 것을 보여줍니다. 이러한 발견은 향후 더 효과적인 강화 학습 방법 개발에 중요한 지침이 될 것입니다.
그러나 DeepSeekMath는 여전히 기하학과 정리 증명 분야에서 상대적으로 약한 성능을 보이며, 모델 규모의 제한으로 인해 퓨 샷 능력에서 GPT-4보다 성능이 떨어지는 한계가 있습니다. 향후 연구에서는 더 고품질의 사전 학습 코퍼스 구축과 효과적인 강화 학습 방법론 개발을 통해 이러한 한계를 극복하고자 합니다.
DeepSeekMath: 오픈 언어 모델의 수학적 추론 한계 극복하기
서론
수학적 추론은 복잡하고 구조화된 특성으로 인해 언어 모델에게 상당한 도전 과제를 제시합니다. 본 논문에서는 DeepSeekMath 7B를 소개합니다. 이 모델은 DeepSeek-Coder-Base-v1.5 7B를 기반으로 Common Crawl에서 추출한 1,200억 개의 수학 관련 토큰과 함께 자연어 및 코드 데이터로 사전 학습을 계속한 모델입니다. DeepSeekMath 7B는 외부 도구나 투표 기법에 의존하지 않고도 경쟁 수준의 MATH 벤치마크에서 51.7%라는 인상적인 점수를 달성했으며, 이는 Gemini-Ultra와 GPT-4의 성능 수준에 근접합니다. DeepSeekMath 7B에서 64개 샘플에 대한 자기 일관성(self-consistency)을 적용하면 MATH에서 60.9%의 성능을 달성합니다.
DeepSeekMath의 수학적 추론 능력은 두 가지 핵심 요소에 기인합니다. 첫째, 세심하게 설계된 데이터 선택 파이프라인을 통해 공개적으로 사용 가능한 웹 데이터의 잠재력을 활용합니다. 둘째, 근접 정책 최적화(Proximal Policy Optimization, PPO)의 변형인 그룹 상대 정책 최적화(Group Relative Policy Optimization, GRPO)를 도입하여 수학적 추론 능력을 향상시키는 동시에 PPO의 메모리 사용량을 최적화합니다.
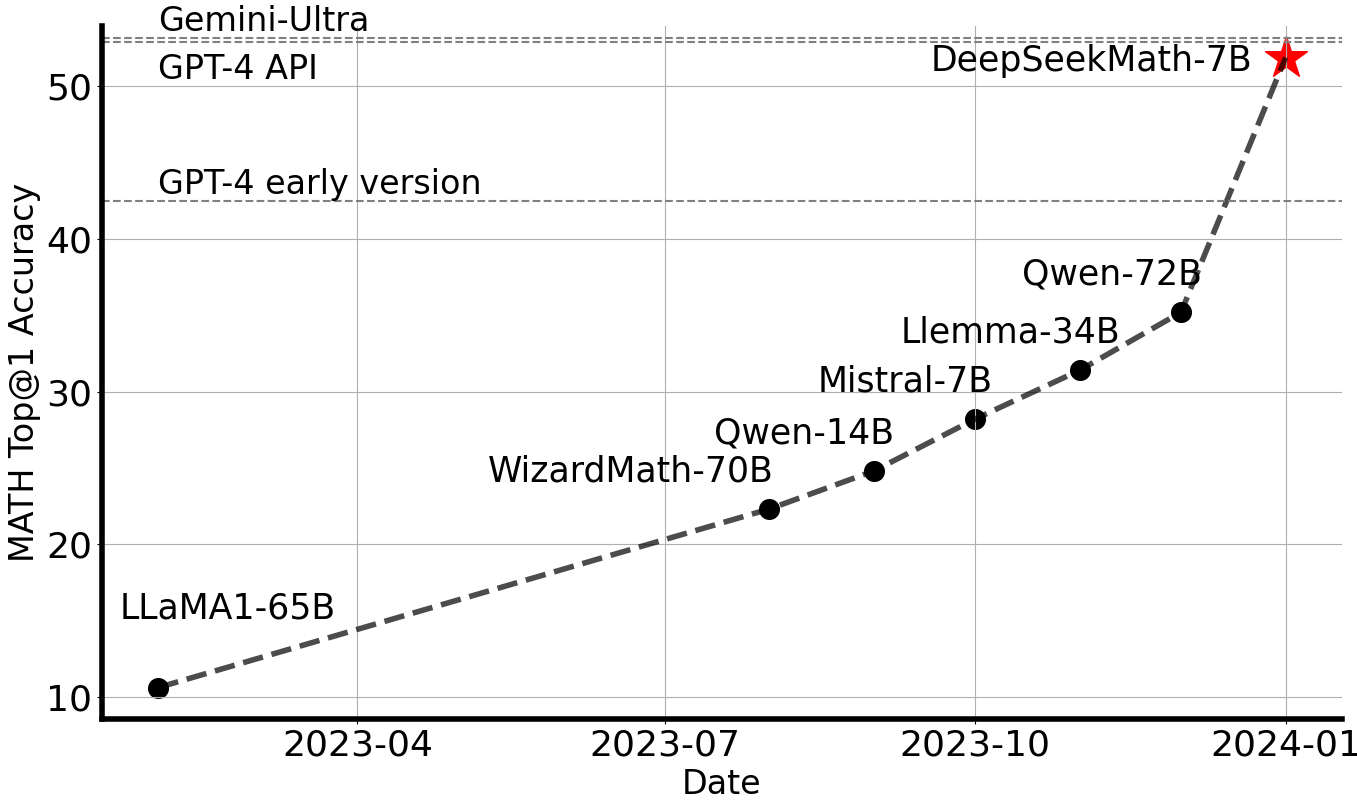
그림 1: 외부 도구와 투표 기법을 사용하지 않고 경쟁 수준의 MATH 벤치마크(Hendrycks 등, 2021)에서 오픈소스 모델의 Top1 정확도.
소개
대규모 언어 모델(LLM)은 인공지능에서 수학적 추론에 대한 접근 방식을 혁신하여 정량적 추론 벤치마크(Hendrycks 등, 2021)와 기하학적 추론 벤치마크(Trinh 등, 2024)에서 상당한 발전을 이루었습니다. 또한 이러한 모델들은 복잡한 수학 문제를 해결하는 데 인간을 지원하는 데 중요한 역할을 했습니다(Tao, 2023). 그러나 GPT-4(OpenAI, 2023)와 Gemini-Ultra(Anil 등, 2023)와 같은 최첨단 모델은 공개적으로 사용할 수 없으며, 현재 접근 가능한 오픈소스 모델은 성능 면에서 상당히 뒤처져 있습니다.
본 연구에서는 오픈소스 모델의 수학적 능력을 크게 뛰어넘고 학술 벤치마크에서 GPT-4의 성능 수준에 근접하는 도메인 특화 언어 모델인 DeepSeekMath를 소개합니다. 이를 위해 Common Crawl(CC)에서 fastText 기반 분류기(Joulin 등, 2016)를 사용하여 추출한 1,200억 개의 수학 토큰으로 구성된 대규모 고품질 사전 학습 코퍼스인 DeepSeekMath Corpus를 생성했습니다. 초기 반복에서 분류기는 OpenWebMath(Paster 등, 2023)의 인스턴스를 긍정적 예시로 사용하여 학습되었으며, 부정적 예시로는 다양한 다른 웹 페이지를 포함했습니다. 이후 분류기를 사용하여 CC에서 추가적인 긍정적 인스턴스를 발굴하고, 이를 인간 주석을 통해 더욱 정제했습니다. 그런 다음 분류기는 이 향상된 데이터셋으로 업데이트되어 성능을 개선했습니다.
평가 결과는 이 대규모 코퍼스가 고품질임을 보여줍니다. 기본 모델인 DeepSeekMath-Base 7B는 GSM8K(Cobbe 등, 2021)에서 64.2%, 경쟁 수준의 MATH 데이터셋(Hendrycks 등, 2021)에서 36.2%를 달성하여 Minerva 540B(Lewkowycz 등, 2022a)를 능가했습니다. 또한 DeepSeekMath Corpus는 다국어를 지원하므로 중국어 수학 벤치마크(Wei 등, 2023; Zhong 등, 2023)에서도 개선이 관찰되었습니다. 저자들은 수학 데이터 처리에 대한 경험이 연구 커뮤니티의 출발점이 될 것이며, 향후 상당한 개선의 여지가 있다고 믿습니다.
DeepSeekMath-Base는 DeepSeek-Coder-Base-v1.5 7B(Guo 등, 2024)로 초기화되었습니다. 저자들은 코드 학습 모델에서 시작하는 것이 일반 LLM에 비해 더 나은 선택임을 발견했습니다. 또한 수학 학습이 MMLU(Hendrycks 등, 2020) 및 BBH 벤치마크(Suzgun 등, 2022)에서 모델 성능을 향상시키는 것을 관찰했는데, 이는 수학적 능력뿐만 아니라 일반적인 추론 능력도 향상시킨다는 것을 나타냅니다.
사전 학습 후, 체인 오브 소트(Wei 등, 2022), 프로그램 오브 소트(Chen 등, 2022; Gao 등, 2023), 도구 통합 추론(Gou 등, 2023) 데이터를 사용하여 DeepSeekMath-Base에 수학적 명령어 튜닝을 적용했습니다. 결과적으로 나온 모델인 DeepSeekMath-Instruct 7B는 모든 7B 경쟁 모델을 능가하고 70B 오픈소스 명령어 튜닝 모델과 비슷한 성능을 보입니다.
또한 근접 정책 최적화(PPO)(Schulman 등, 2017)의 변형 강화 학습(RL) 알고리즘인 그룹 상대 정책 최적화(GRPO)를 소개합니다. GRPO는 비평 모델을 사용하지 않고 대신 그룹 점수에서 기준선을 추정하여 학습 리소스를 크게 줄입니다. 영어 명령어 튜닝 데이터의 하위 집합만을 사용하여 GRPO는 강력한 DeepSeekMath-Instruct에 비해 상당한 개선을 얻었습니다. 이는 도메인 내(GSM8K: 82.9% → 88.2%, MATH: 46.8% → 51.7%) 및 도메인 외 수학 작업(예: CMATH: 84.6% → 88.8%) 모두에서 강화 학습 단계 동안 개선되었습니다.
저자들은 또한 거부 샘플링 미세 조정(RFT)(Yuan 등, 2023a), 직접 선호도 최적화(DPO)(Rafailov 등, 2023), PPO 및 GRPO와 같은 다양한 방법을 이해하기 위한 통합 패러다임을 제공합니다. 이러한 통합 패러다임을 기반으로, 저자들은 이러한 모든 방법이 직접적이거나 단순화된 RL 기술로 개념화된다는 것을 발견했습니다. 또한 온라인 대 오프라인 학습, 결과 대 과정 감독, 단일 턴 대 반복적 RL 등과 같은 광범위한 실험을 수행하여 이 패러다임의 필수 요소를 심층적으로 조사했습니다. 마지막으로, RL이 명령어 튜닝 모델의 성능을 향상시키는 이유를 설명하고, 이 통합 패러다임을 기반으로 더 효과적인 RL을 달성하기 위한 잠재적 방향을 요약합니다.
기여
본 연구의 기여는 확장 가능한 수학 사전 학습과 강화 학습의 탐색 및 분석을 포함합니다.
대규모 수학 사전 학습
-
본 연구는 공개적으로 접근 가능한 Common Crawl 데이터가 수학적 목적에 유용한 정보를 포함하고 있다는 설득력 있는 증거를 제공합니다. 세심하게 설계된 데이터 선택 파이프라인을 구현하여 수학적 내용으로 필터링된 웹 페이지에서 1,200억 토큰의 고품질 데이터셋인 DeepSeekMath Corpus를 성공적으로 구축했습니다. 이는 Minerva(Lewkowycz 등, 2022a)에서 사용된 수학 웹 페이지의 거의 7배, 최근 출시된 OpenWebMath(Paster 등, 2023)의 9배에 해당하는 규모입니다.
-
사전 학습된 기본 모델인 DeepSeekMath-Base 7B는 Minerva 540B(Lewkowycz 등, 2022a)와 비슷한 성능을 달성하여, 매개변수 수가 수학적 추론 능력의 유일한 핵심 요소가 아님을 보여줍니다. 고품질 데이터로 사전 학습된 더 작은 모델도 강력한 성능을 달성할 수 있습니다.
-
수학 학습 실험에서 얻은 발견을 공유합니다. 수학 학습 전에 코드 학습을 하면 도구 사용 여부와 관계없이 모델의 수학 문제 해결 능력이 향상됩니다. 이는 오랫동안 제기된 질문인 “코드 학습이 추론 능력을 향상시키는가?”에 대한 부분적인 답변을 제공합니다. 저자들은 적어도 수학적 추론에 있어서는 그렇다고 믿습니다.
-
arXiv 논문에 대한 학습이 특히 많은 수학 관련 논문에서 일반적이지만, 본 논문에서 채택된 모든 수학 벤치마크에서 주목할 만한 개선을 가져오지 않았습니다.
강화 학습의 탐색 및 분석
-
효율적이고 효과적인 강화 학습 알고리즘인 그룹 상대 정책 최적화(GRPO)를 소개합니다. GRPO는 비평 모델을 사용하지 않고 대신 그룹 점수에서 기준선을 추정하여 근접 정책 최적화(PPO)에 비해 학습 리소스를 크게 줄입니다.
-
GRPO가 명령어 튜닝 데이터만을 사용하여 명령어 튜닝 모델인 DeepSeekMath-Instruct의 성능을 크게 향상시킨다는 것을 보여줍니다. 또한 강화 학습 과정에서 도메인 외 성능이 향상되는 것을 관찰했습니다.
-
RFT, DPO, PPO 및 GRPO와 같은 다양한 방법을 이해하기 위한 통합 패러다임을 제공합니다. 또한 온라인 대 오프라인 학습, 결과 대 과정 감독, 단일 턴 대 반복적 강화 학습 등과 같은 광범위한 실험을 수행하여 이 패러다임의 필수 요소를 심층적으로 조사했습니다.
-
통합 패러다임을 기반으로 강화 학습의 효과 뒤에 있는 이유를 탐색하고, LLM의 더 효과적인 강화 학습을 달성하기 위한 몇 가지 잠재적 방향을 요약합니다.
평가 및 지표 요약
영어 및 중국어 수학적 추론
저자들은 초등학교 수준부터 대학 수준까지의 수학 문제를 다루는 영어 및 중국어 벤치마크에서 모델에 대한 포괄적인 평가를 수행했습니다. 영어 벤치마크에는 GSM8K(Cobbe 등, 2021), MATH(Hendrycks 등, 2021), SAT(Azerbayev 등, 2023), OCW Courses(Lewkowycz 등, 2022a), MMLU-STEM(Hendrycks 등, 2020)이 포함됩니다. 중국어 벤치마크에는 MGSM-zh(Shi 등, 2023), CMATH(Wei 등, 2023), Gaokao-MathCloze(Zhong 등, 2023), Gaokao-MathQA(Zhong 등, 2023)가 포함됩니다.
모델이 도구 사용 없이 자체 포함된 텍스트 솔루션을 생성하는 능력과 Python을 사용하여 문제를 해결하는 능력을 평가했습니다. 영어 벤치마크에서 DeepSeekMath-Base는 비공개 Minerva 540B(Lewkowycz 등, 2022a)와 경쟁력이 있으며, 수학 사전 학습 여부와 관계없이 모든 오픈소스 기본 모델(예: Mistral 7B(Jiang 등, 2023) 및 Llemma-34B(Azerbayev 등, 2023))을 상당한 차이로 능가합니다. 특히 DeepSeekMath-Base는 중국어 벤치마크에서 우수한 성능을 보이는데, 이는 이전 연구(Lewkowycz 등, 2022a; Azerbayev 등, 2023)와 달리 영어로만 된 수학 사전 학습 데이터를 수집하지 않고 고품질의 비영어 데이터도 포함했기 때문일 가능성이 높습니다.
수학적 명령어 튜닝과 강화 학습을 통해 결과적으로 나온 모델인 DeepSeekMath-Instruct와 DeepSeekMath-RL은 강력한 성능을 보여주며, 오픈소스 커뮤니티 내에서 처음으로 경쟁 수준의 MATH 데이터셋에서 50% 이상의 정확도를 달성했습니다.
형식적 수학
저자들은 Isabelle(Wenzel 등, 2008)을 증명 보조 도구로 선택한 miniF2F(Zheng 등, 2021)에서 Jiang 등(2022)의 비형식적-형식적 정리 증명 작업을 사용하여 DeepSeekMath-Base를 평가했습니다. DeepSeekMath-Base는 강력한 퓨 샷 자동 형식화 성능을 보여줍니다.
자연어 이해, 추론 및 코드
모델의 일반적인 이해, 추론 및 코딩 능력에 대한 포괄적인 프로필을 구축하기 위해 저자들은 DeepSeekMath-Base를 다양한 주제를 다루는 57개의 객관식 작업으로 구성된 Massive Multitask Language Understanding(MMLU) 벤치마크(Hendrycks 등, 2020), 대부분 다단계 추론이 필요한 23개의 도전적인 작업으로 구성된 BIG-Bench Hard(BBH)(Suzgun 등, 2022), 그리고 코드 언어 모델을 평가하는 데 널리 사용되는 HumanEval(Chen 등, 2021) 및 MBPP(Austin 등, 2021)에서 평가했습니다. 수학 사전 학습은 언어 이해와 추론 성능 모두에 도움이 됩니다.
수학 사전 학습
데이터 수집 및 오염 제거
이 섹션에서는 Common Crawl에서 DeepSeekMath 코퍼스를 구축하는 과정을 설명합니다. 그림 2에서 볼 수 있듯이, 시드 코퍼스(예: 고품질의 소규모 수학 관련 데이터셋 모음)에서 시작하여 Common Crawl에서 대규모 수학 코퍼스를 체계적으로 수집하는 반복적인 파이프라인을 제시합니다. 이 접근 방식은 코딩과 같은 다른 도메인에도 적용할 수 있습니다.
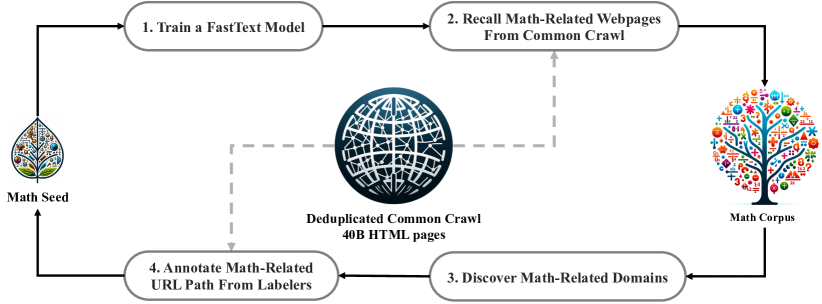
그림 2: Common Crawl에서 수학적 웹 페이지를 수집하는 반복적인 파이프라인.
먼저, 고품질의 수학적 웹 텍스트 모음인 OpenWebMath(Paster 등, 2023)를 초기 시드 코퍼스로 선택합니다. 이 코퍼스를 사용하여 더 많은 OpenWebMath와 유사한 수학적 웹 페이지를 검색하기 위한 fastText 모델(Joulin 등, 2016)을 학습시킵니다. 구체적으로, 시드 코퍼스에서 500,000개의 데이터 포인트를 긍정적인 학습 예시로 무작위로 선택하고, Common Crawl에서 다른 500,000개의 웹 페이지를 부정적인 예시로 선택합니다. 학습을 위해 오픈소스 라이브러리인 fastText를 사용하며, 벡터 차원을 256, 학습률을 0.1, 단어 n-그램의 최대 길이를 3, 단어 출현 최소 횟수를 3, 학습 에포크 수를 3으로 설정합니다.
원본 Common Crawl의 크기를 줄이기 위해 URL 기반 중복 제거 및 근접 중복 제거 기술을 사용하여 40B HTML 웹 페이지로 축소합니다. 그런 다음 fastText 모델을 사용하여 중복 제거된 Common Crawl에서 수학적 웹 페이지를 검색합니다. 저품질의 수학적 콘텐츠를 필터링하기 위해 fastText 모델이 예측한 점수에 따라 수집된 페이지를 순위화하고, 상위 순위의 페이지만 보존합니다. 보존되는 데이터의 양은 상위 40B, 80B, 120B, 160B 토큰에 대한 사전 학습 실험을 통해 평가됩니다. 첫 번째 반복에서는 상위 40B 토큰을 유지하기로 결정합니다.
첫 번째 데이터 수집 반복 후에도 많은 수학적 웹 페이지가 수집되지 않은 상태로 남아 있는데, 이는 주로 fastText 모델이 충분한 다양성이 부족한 긍정적 예시 세트로 학습되었기 때문입니다. 따라서 시드 코퍼스를 풍부하게 하기 위해 추가적인 수학적 웹 소스를 식별하여 fastText 모델을 최적화합니다. 구체적으로, 먼저 전체 Common Crawl을 동일한 기본 URL을 공유하는 웹 페이지인 개별 도메인으로 구성합니다. 각 도메인에 대해 첫 번째 반복에서 수집된 웹 페이지의 비율을 계산합니다. 웹 페이지의 10% 이상이 수집된 도메인은 수학 관련(예: mathoverflow.net)으로 분류됩니다. 이후 이러한 식별된 도메인 내에서 수학적 콘텐츠와 관련된 URL을 수동으로 주석 처리합니다(예: mathoverflow.net/questions). 이러한 URL에 연결되어 있지만 아직 수집되지 않은 웹 페이지는 시드 코퍼스에 추가됩니다. 이 접근 방식을 통해 더 많은 긍정적인 예시를 수집할 수 있으며, 이를 통해 다음 반복에서 더 많은 수학적 데이터를 검색할 수 있는 개선된 fastText 모델을 학습시킬 수 있습니다.
데이터 수집의 네 번째 반복 후, 총 35.5M개의 수학적 웹 페이지를 수집하여 120B 토큰을 확보했습니다. 네 번째 반복에서는 데이터의 거의 98%가 이미 세 번째 반복에서 수집되었음을 확인하고 데이터 수집을 중단하기로 결정했습니다.
벤치마크 오염을 방지하기 위해 Guo 등(2024)의 방법을 따라 GSM8K(Cobbe 등, 2021)와 MATH(Hendrycks 등, 2021)와 같은 영어 수학 벤치마크와 CMATH(Wei 등, 2023)와 AGIEval(Zhong 등, 2023)과 같은 중국어 벤치마크의 질문이나 답변을 포함하는 웹 페이지를 필터링합니다. 필터링 기준은 다음과 같습니다. 평가 벤치마크의 하위 문자열과 정확히 일치하는 10-그램 문자열을 포함하는 텍스트 세그먼트는 수학 학습 코퍼스에서 제거됩니다. 10-그램보다 짧지만 최소 3-그램 이상인 벤치마크 텍스트의 경우, 정확한 매칭을 사용하여 오염된 웹 페이지를 필터링합니다.
DeepSeekMath 코퍼스의 품질 검증
DeepSeekMath 코퍼스가 최근 출시된 수학 학습 코퍼스와 어떻게 비교되는지 조사하기 위해 사전 학습 실험을 실행합니다.
• MathPile(Wang 등, 2023c): 교과서, 위키피디아, ProofWiki, CommonCrawl, StackExchange, arXiv에서 집계된 다중 소스 코퍼스(8.9B 토큰)로, 대부분(85% 이상)은 arXiv에서 가져온 것입니다.
• OpenWebMath(Paster 등, 2023): 수학적 콘텐츠로 필터링된 CommonCrawl 데이터로, 총 13.6B 토큰입니다.
• Proof-Pile-2(Azerbayev 등, 2023): OpenWebMath, AlgebraicStack(10.3B 토큰의 수학적 코드), arXiv 논문(28.0B 토큰)으로 구성된 수학적 코퍼스입니다. Proof-Pile-2에 대한 실험에서는 Azerbayev 등(2023)을 따라 arXiv:Web:Code 비율을 2:4:1로 사용합니다.
학습 설정
1.3B 매개변수를 가진 일반 사전 학습 언어 모델에 수학 학습을 적용합니다. 이 모델은 DeepSeek LLM(DeepSeek-AI, 2024)과 동일한 프레임워크를 공유하며, DeepSeek-LLM 1.3B로 표시됩니다. 각 수학적 코퍼스에 대해 별도로 150B 토큰에 대해 모델을 학습시킵니다. 모든 실험은 효율적이고 가벼운 HAI-LLM(High-flyer, 2023) 학습 프레임워크를 사용하여 수행됩니다.
DeepSeek LLM의 학습 관행을 따라, $\beta_{1}=0.9$, $\beta_{2}=0.95$, $\mathrm{weight\ decay}=0.1$을 가진 AdamW 옵티마이저(Loshchilov와 Hutter, 2017)를 사용하며, 다단계 학습률 스케줄을 함께 사용합니다. 이 스케줄에서 학습률은 2,000번의 웜업 단계 후에 최고점에 도달하고, 학습 과정의 80% 후에 31.6%로 감소하며, 학습 과정의 90% 후에 최고점의 10.0%로 더 감소합니다. 학습률의 최대값을 5.3e-4로 설정하고, 4K 컨텍스트 길이로 4M 토큰의 배치 크기를 사용합니다.
평가 결과
DeepSeekMath 코퍼스는 고품질이며, 다국어 수학적 콘텐츠를 포함하고, 크기가 가장 큽니다.
• 고품질: Wei 등(2022)의 퓨 샷 체인 오브 소트 프롬프팅을 사용하여 8개의 수학적 벤치마크에서 다운스트림 성능을 평가합니다. 표 1에서 볼 수 있듯이, DeepSeekMath 코퍼스에서 학습된 모델의 성능이 명확하게 앞서고 있습니다. 그림 3은 DeepSeekMath 코퍼스에서 학습된 모델이 50B 토큰(Proof-Pile-2의 1회 전체 에포크)에서 Proof-Pile-2보다 더 나은 성능을 보여주며, 이는 DeepSeekMath 코퍼스의 평균 품질이 더 높다는 것을 나타냅니다.
• 다국어: DeepSeekMath 코퍼스는 여러 언어의 데이터를 포함하며, 주로 영어와 중국어가 가장 많이 표현됩니다. 표 1에서 볼 수 있듯이, DeepSeekMath 코퍼스에서의 학습은 영어와 중국어 모두에서 수학적 추론 성능을 향상시킵니다. 반면, 주로 영어 중심인 기존의 수학적 코퍼스는 개선이 제한적이며 중국어 수학적 추론 성능을 저해할 수도 있습니다.
• 대규모: DeepSeekMath 코퍼스는 기존 수학적 코퍼스보다 몇 배 더 큽니다. 그림 3에서 볼 수 있듯이, DeepSeekMath 코퍼스에서 학습된 DeepSeek-LLM 1.3B는 더 가파른 학습 곡선과 더 지속적인 개선을 보여줍니다. 반면, 기준 코퍼스는 훨씬 작으며, 학습 중에 이미 여러 라운드를 반복했으며, 결과적으로 모델 성능이 빠르게 정체됩니다.
| 수학 코퍼스 | 크기 | 영어 벤치마크 | 중국어 벤치마크 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GSM8K | MATH | OCW | SAT | MMLU STEM | CMATH | Gaokao MathCloze | Gaokao MathQA | ||
| 수학 학습 없음 | N/A | 2.9% | 3.0% | 2.9% | 15.6% | 19.5% | 12.3% | 0.8% | 17.9% |
| MathPile | 8.9B | 2.7% | 3.3% | 2.2% | 12.5% | 15.7% | 1.2% | 0.0% | 2.8% |
| OpenWebMath | 13.6B | 11.5% | 8.9% | 3.7% | 31.3% | 29.6% | 16.8% | 0.0% | 14.2% |
| Proof-Pile-2 | 51.9B | 14.3% | 11.2% | 3.7% | 43.8% | 29.2% | 19.9% | 5.1% | 11.7% |
| DeepSeekMath 코퍼스 | 120.2B | 23.8% | 13.6% | 4.8% | 56.3% | 33.1% | 41.5% | 5.9% | 23.6% |
표 1: 다양한 수학적 코퍼스에서 학습된 DeepSeek-LLM 1.3B의 성능, 퓨 샷 체인 오브 소트 프롬프팅을 사용하여 평가됨. 코퍼스 크기는 100K 어휘 크기의 토크나이저를 사용하여 계산됨.
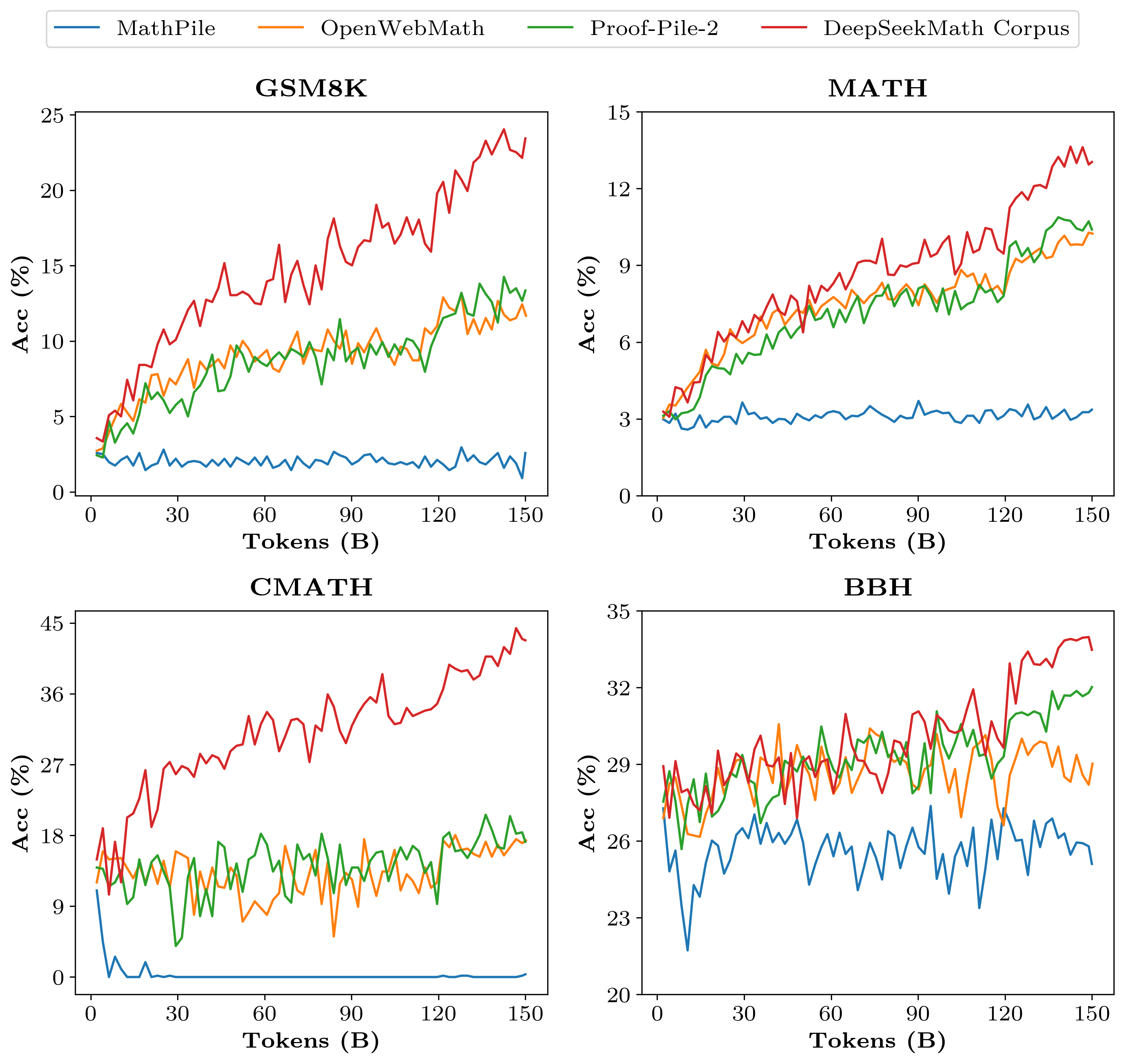
그림 3: 다양한 수학적 코퍼스에서 학습된 DeepSeek-LLM 1.3B의 벤치마크 곡선.
DeepSeekMath-Base 7B의 학습 및 평가
이 섹션에서는 특히 수학에서 강력한 추론 능력을 가진 기본 모델인 DeepSeekMath-Base 7B를 소개합니다. 이 모델은 DeepSeek-Coder-Base-v1.5 7B(Guo 등, 2024)로 초기화되어 500B 토큰에 대해 학습되었습니다. 데이터 분포는 다음과 같습니다. 56%는 DeepSeekMath 코퍼스에서, 4%는 AlgebraicStack에서, 10%는 arXiv에서, 20%는 Github 코드에서, 나머지 10%는 영어와 중국어 모두의 Common Crawl에서 가져온 자연어 데이터입니다.
주로 앞의 섹션에 명시된 학습 설정을 채택하되, 학습률의 최대값을 4.2e-4로 설정하고 10M 토큰의 배치 크기를 사용합니다.
DeepSeekMath-Base 7B의 수학적 능력에 대한 포괄적인 평가를 수행하며, 외부 도구에 의존하지 않고 자체 포함된 수학적 솔루션을 생성하는 능력, 도구를 사용하여 수학 문제를 해결하는 능력, 형식적 정리 증명을 수행하는 능력에 초점을 맞춥니다. 수학을 넘어서, 자연어 이해, 추론, 프로그래밍 기술을 포함한 기본 모델의 더 일반적인 프로필도 제공합니다.
단계별 추론을 통한 수학 문제 해결
DeepSeekMath-Base의 퓨 샷 체인 오브 소트 프롬프팅(Wei 등, 2022)을 사용한 수학 문제 해결 성능을 영어와 중국어로 된 8개의 벤치마크에서 평가합니다. 이러한 벤치마크는 정량적 추론(예: GSM8K(Cobbe 등, 2021), MATH(Hendrycks 등, 2021), CMATH(Wei 등, 2023))과 객관식 문제(예: MMLU-STEM(Hendrycks 등, 2020)과 Gaokao-MathQA(Zhong 등, 2023))를 포함하며, 초등학교부터 대학 수준의 복잡성까지 다양한 수학 분야를 다룹니다.
표 2에서 볼 수 있듯이, DeepSeekMath-Base 7B는 오픈소스 기본 모델(널리 사용되는 일반 모델인 Mistral 7B(Jiang 등, 2023)와 최근 출시된 Proof-Pile-2(Azerbayev 등, 2023)에서 수학 학습을 거친 Llemma 34B(Azerbayev 등, 2023) 포함) 중에서 8개의 모든 벤치마크에서 성능을 선도합니다. 특히, 경쟁 수준의 MATH 데이터셋에서 DeepSeekMath-Base는 기존 오픈소스 기본 모델보다 10% 이상의 절대적인 차이로 앞서며, PaLM(Lewkowycz 등, 2022b)을 기반으로 하고 수학적 텍스트에 대해 추가로 학습된 77배 더 큰 비공개 기본 모델인 Minerva 540B(Lewkowycz 등, 2022a)를 능가합니다.
| 모델 | 크기 | 영어 벤치마크 | 중국어 벤치마크 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| GSM8K | MATH | OCW SAT | MMLU STEM | CMATH | Gaokao MathCloze | Gaokao MathQA | |||
| 비공개 기본 모델 | |||||||||
| Minerva | 7B | 16.2% | 14.1% | 7.7% | - | 35.6% | - | - | - |
| Minerva | 62B | 52.4% | 27.6% | 12.0% | - | 53.9% | - | - | - |
| Minerva | 540B | 58.8% | 33.6% | 17.6% | - | 63.9% | - | - | - |
| 오픈소스 기본 모델 | |||||||||
| Mistral | 7B | 40.3% | 14.3% | 9.2% | 71.9% | 51.1% | 44.9% | 5.1% | 23.4% |
| Llemma | 7B | 37.4% | 18.1% | 6.3% | 59.4% | 43.1% | 43.4% | 11.9% | 23.6% |
| Llemma | 34B | 54.0% | 25.3% | 10.3% | 71.9% | 52.9% | 56.1% | 11.9% | 26.2% |
| DeepSeekMath-Base | 7B | 64.2% | 36.2% | 15.4% | 84.4% | 56.5% | 71.7% | 20.3% | 35.3% |
표 2: 영어 및 중국어 수학적 벤치마크에서 DeepSeekMath-Base 7B와 강력한 기본 모델 간의 비교. 모델은 체인 오브 소트 프롬프팅으로 평가됨. Minerva 결과는 Lewkowycz 등(2022a)에서 인용됨.
도구 사용을 통한 수학 문제 해결
GSM8K와 MATH에서 퓨 샷 프로그램 오브 소트 프롬프팅(Chen 등, 2022; Gao 등, 2023)을 사용하여 프로그램 지원 수학적 추론을 평가합니다. 모델은 각 문제를 math와 sympy와 같은 라이브러리를 복잡한 계산에 활용할 수 있는 Python 프로그램을 작성하여 해결하도록 프롬프트됩니다. 프로그램의 실행 결과가 답으로 평가됩니다. 표 3에서 볼 수 있듯이, DeepSeekMath-Base 7B는 이전 최첨단 Llemma 34B를 능가합니다.
| 모델 | 크기 | 도구를 사용한 문제 해결 | 비형식적-형식적 증명 | ||
|---|---|---|---|---|---|
| GSM8K+Python | MATH+Python | miniF2F-valid | miniF2F-test | ||
| Mistral | 7B | 48.5% | 18.2% | 18.9% | 18.0% |
| CodeLlama | 7B | 27.1% | 17.2% | 16.3% | 17.6% |
| CodeLlama | 34B | 52.7% | 23.5% | 18.5% | 18.0% |
| Llemma | 7B | 41.0% | 18.6% | 20.6% | 22.1% |
| Llemma | 34B | 64.6% | 26.3% | 21.0% | 21.3% |
| DeepSeekMath-Base | 7B | 66.9% | 31.4% | 25.8% | 24.6% |
표 3: 도구를 사용한 수학 문제 해결 능력과 Isabelle에서 비형식적-형식적 정리 증명을 수행하는 능력에 대한 기본 모델의 퓨 샷 평가.
형식적 수학
형식적 증명 자동화는 수학적 증명의 정확성과 신뢰성을 보장하고 효율성을 향상시키는 데 유용하며, 최근 몇 년간 관심이 증가하고 있습니다. DeepSeekMath-Base 7B를 Jiang 등(2022)의 비형식적-형식적 증명 작업에서 평가합니다. 이 작업은 비형식적 진술, 진술의 형식적 대응물, 비형식적 증명을 기반으로 형식적 증명을 생성하는 것입니다. 형식적 올림피아드 수준의 수학을 위한 벤치마크인 miniF2F(Zheng 등, 2021)에서 평가하며, 퓨 샷 프롬프팅으로 각 문제에 대한 Isabelle의 형식적 증명을 생성합니다. Jiang 등(2022)을 따라, 모델을 활용하여 증명 스케치를 생성하고, 오프더쉘프 자동화된 증명기인 Sledgehammer(Paulson, 2010)를 실행하여 누락된 세부 사항을 채웁니다. 표 3에서 볼 수 있듯이, DeepSeekMath-Base 7B는 증명 자동 형식화에서 강력한 성능을 보여줍니다.
자연어 이해, 추론 및 코드
MMLU(Hendrycks 등, 2020)에서의 자연어 이해, BBH(Suzgun 등, 2022)에서의 추론, HumanEval(Chen 등, 2021)과 MBPP(Austin 등, 2021)에서의 코딩 능력에 대한 모델 성능을 평가합니다. 표 4에서 볼 수 있듯이, DeepSeekMath-Base 7B는 전신인 DeepSeek-Coder-Base-v1.5(Guo 등, 2024)에 비해 MMLU와 BBH에서 성능이 크게 향상되어 수학 학습이 언어 이해와 추론에 미치는 긍정적인 영향을 보여줍니다. 또한, 지속적인 학습을 위해 코드 토큰을 포함함으로써 DeepSeekMath-Base 7B는 두 코딩 벤치마크에서 DeepSeek-Coder-Base-v1.5의 성능을 효과적으로 유지합니다. 전반적으로, DeepSeekMath-Base 7B는 세 가지 추론 및 코딩 벤치마크에서 일반 모델인 Mistral 7B(Jiang 등, 2023)를 크게 능가합니다.
| 모델 | 크기 | MMLU | BBH | HumanEval (Pass@1) | MBPP (Pass@1) |
|---|---|---|---|---|---|
| Mistral | 7B | 62.4% | 55.7% | 28.0% | 41.4% |
| DeepSeek-Coder-Base-v1.5† | 7B | 42.9% | 42.9% | 40.2% | 52.6% |
| DeepSeek-Coder-Base-v1.5 | 7B | 49.1% | 55.2% | 43.2% | 60.4% |
| DeepSeekMath-Base | 7B | 54.9% | 59.5% | 40.9% | 52.6% |
표 4: 자연어 이해, 추론 및 코드 벤치마크에 대한 평가. DeepSeek-Coder-Base-v1.5 †는 학습률 감소 직전의 체크포인트로, DeepSeekMath-Base를 학습하는 데 사용됨. MMLU와 BBH에서는 퓨 샷 체인 오브 소트 프롬프팅을 사용함. HumanEval과 MBPP에서는 각각 제로 샷 설정과 퓨 샷 설정에서 모델 성능을 평가함.
지도 학습 미세 조정
SFT 데이터 큐레이션
DeepSeekMath 연구팀은 영어와 중국어로 된 다양한 수학 분야와 난이도를 포괄하는 수학적 명령어 튜닝 데이터셋을 구축했습니다. 이 데이터셋은 체인 오브 소트(CoT)(Wei 등, 2022), 프로그램 오브 소트(PoT)(Chen 등, 2022; Gao 등, 2023), 그리고 도구 통합 추론 형식(Gou 등, 2023)으로 문제와 해답을 쌍으로 구성했습니다. 전체 학습 예시의 수는 776K개에 달합니다.
영어 수학 데이터셋의 경우, 연구팀은 GSM8K와 MATH 문제에 도구 통합 솔루션으로 주석을 달았으며, MathInstruct(Yue 등, 2023)의 일부와 Lila-OOD(Mishra 등, 2022) 학습 세트를 채택했습니다. 이러한 문제들은 CoT 또는 PoT로 해결되었습니다. 영어 컬렉션은 대수학, 확률, 정수론, 미적분학, 기하학 등 다양한 수학 분야를 포괄합니다.
중국어 수학 데이터셋의 경우, 연구팀은 선형 방정식과 같은 76개의 하위 주제를 포괄하는 중국 K-12 수학 문제를 수집했으며, 이 문제들에는 CoT와 도구 통합 추론 형식 모두로 주석이 달렸습니다.
DeepSeekMath-Instruct 7B의 학습 및 평가
이 섹션에서는 DeepSeekMath-Base를 기반으로 수학적 명령어 튜닝을 거친 DeepSeekMath-Instruct 7B를 소개합니다. 학습 예시는 최대 컨텍스트 길이인 4K 토큰에 도달할 때까지 무작위로 연결되었습니다. 모델은 256의 배치 크기와 5e-5의 일정한 학습률로 500 스텝 동안 학습되었습니다.
연구팀은 도구 사용 여부와 관계없이 영어와 중국어로 된 4개의 정량적 추론 벤치마크에서 모델의 수학적 성능을 평가했습니다. 이들은 당시 선도적인 모델들과 비교했습니다.
비공개 소스 모델에는 다음이 포함됩니다.
- GPT 계열 중 GPT-4(OpenAI, 2023)와 GPT-4 Code Interpreter가 가장 뛰어난 성능을 보였습니다.
- Gemini Ultra와 Pro(Anil 등, 2023)
- Inflection-2(Inflection AI, 2023)
- Grok-1
- 중국 기업들이 최근 출시한 모델들로, Baichuan-3와 GLM 계열의 최신 GLM-4(Du 등, 2022)가 있습니다.
이러한 모델들은 일반적인 목적을 위한 것으로, 대부분 일련의 정렬 절차를 거쳤습니다.
오픈소스 모델에는 다음이 포함됩니다.
- DeepSeek-LLM-Chat 67B(DeepSeek-AI, 2024)와 같은 일반 모델
- Qwen 72B(Bai 등, 2023)
- SeaLLM-v2 7B(Nguyen 등, 2023)
- ChatGLM3 6B(ChatGLM3 Team, 2023)
또한 수학 분야에서 향상된 모델들도 포함됩니다.
- InternLM2-Math 20B - InternLM2를 기반으로 수학 학습 후 명령어 튜닝을 거쳤습니다.
- Math-Shepherd-Mistral 7B - Mistral 7B(Jiang 등, 2023)에 프로세스 지도 보상 모델을 사용한 PPO 학습(Schulman 등, 2017)을 적용했습니다.
- WizardMath 시리즈(Luo 등, 2023) - Mistral 7B와 Llama-2 70B(Touvron 등, 2023)의 수학적 추론 능력을 진화-명령어(AI가 진화시킨 명령어를 사용하는 명령어 튜닝의 한 버전)와 PPO 학습을 통해 향상시켰으며, 주로 GSM8K와 MATH에서 가져온 학습 문제를 사용했습니다.
- MetaMath 70B(Yu 등, 2023) - GSM8K와 MATH의 증강된 버전으로 미세 조정된 Llama-2 70B입니다.
- ToRA 34B(Gou 등, 2023) - 도구 통합 수학적 추론을 수행하도록 미세 조정된 CodeLlama 34B입니다.
- MAmmoTH 70B(Yue 등, 2023) - MathInstruct에 대해 명령어 튜닝된 Llama-2 70B입니다.
표 5에서 볼 수 있듯이, 도구 사용이 허용되지 않는 평가 설정에서 DeepSeekMath-Instruct 7B는 단계별 추론에 강력한 성능을 보여줍니다. 특히 경쟁 수준의 MATH 데이터셋에서 이 모델은 모든 오픈소스 모델과 대부분의 독점 모델(예: Inflection-2 및 Gemini Pro)을 최소 9% 절대적인 차이로 능가합니다. 이는 상당히 더 큰 모델(예: Qwen 72B)이나 수학 중심의 강화 학습을 통해 특별히 향상된 모델(예: WizardMath-v1.1 7B)과 비교해도 마찬가지입니다. DeepSeekMath-Instruct는 MATH에서 중국 독점 모델인 GLM-4와 Baichuan-3와 경쟁하지만, 여전히 GPT-4와 Gemini Ultra보다는 성능이 떨어집니다.
모델이 문제 해결을 위해 자연어 추론과 프로그램 기반 도구 사용을 통합할 수 있는 평가 설정에서, DeepSeekMath-Instruct 7B는 MATH에서 약 60%의 정확도에 접근하여 모든 기존 오픈소스 모델을 능가합니다. 다른 벤치마크에서도 이 모델은 10배 더 큰 이전 최첨단 모델인 DeepSeek-LLM-Chat 67B와 경쟁력이 있습니다.
| 모델 | 크기 | 영어 벤치마크 | 중국어 벤치마크 | |||
|---|---|---|---|---|---|---|
| GSM8K | MATH | MGSM-zh | CMATH | |||
| 체인 오브 소트 추론 | ||||||
| 비공개 소스 모델 | ||||||
| Gemini Ultra | - | 94.4% | 53.2% | - | - | |
| GPT-4 | - | 92.0% | 52.9% | - | 86.0% | |
| Inflection-2 | - | 81.4% | 34.8% | - | - | |
| GPT-3.5 | - | 80.8% | 34.1% | - | 73.8% | |
| Gemini Pro | - | 86.5% | 32.6% | - | - | |
| Grok-1 | - | 62.9% | 23.9% | - | - | |
| Baichuan-3 | - | 88.2% | 49.2% | - | - | |
| GLM-4 | - | 87.6% | 47.9% | - | - | |
| 오픈소스 모델 | ||||||
| InternLM2-Math | 20B | 82.6% | 37.7% | - | - | |
| Qwen | 72B | 78.9% | 35.2% | - | - | |
| Math-Shepherd-Mistral | 7B | 84.1% | 33.0% | - | - | |
| WizardMath-v1.1 | 7B | 83.2% | 33.0% | - | - | |
| DeepSeek-LLM-Chat | 67B | 84.1% | 32.6% | 74.0% | 80.3% | |
| MetaMath | 70B | 82.3% | 26.6% | 66.4% | 70.9% | |
| SeaLLM-v2 | 7B | 78.2% | 27.5% | 64.8% | - | |
| ChatGLM3 | 6B | 72.3% | 25.7% | - | - | |
| WizardMath-v1.0 | 70B | 81.6% | 22.7% | 64.8% | 65.4% | |
| DeepSeekMath-Instruct | 7B | 82.9% | 46.8% | 73.2% | 84.6% | |
| DeepSeekMath-RL | 7B | 88.2% | 51.7% | 79.6% | 88.8% | |
| 도구 통합 추론 | ||||||
| 비공개 소스 모델 | ||||||
| GPT-4 Code Interpreter | - | 97.0% | 69.7% | - | - | |
| 오픈소스 모델 | ||||||
| InternLM2-Math | 20B | 80.7% | 54.3% | - | - | |
| DeepSeek-LLM-Chat | 67B | 86.7% | 51.1% | 76.4% | 85.4% | |
| ToRA | 34B | 80.7% | 50.8% | 41.2% | 53.4% | |
| MAmmoTH | 70B | 76.9% | 41.8% | - | - | |
| DeepSeekMath-Instruct | 7B | 83.7% | 57.4% | 72.0% | 84.3% | |
| DeepSeekMath-RL | 7B | 86.7% | 58.8% | 78.4% | 87.6% |
표 5: 영어 및 중국어 벤치마크에서 체인 오브 소트와 도구 통합 추론을 모두 사용한 오픈소스 및 비공개 소스 모델의 성능. 회색으로 표시된 점수는 32개 후보에 대한 다수결 투표를 나타내며, 나머지는 Top1 점수입니다. DeepSeekMath-RL 7B는 7B부터 70B까지의 모든 오픈소스 모델뿐만 아니라 대부분의 비공개 소스 모델을 능가합니다. DeepSeekMath-RL 7B는 GSM8K와 MATH의 체인 오브 소트 형식 명령어 튜닝 데이터에 대해서만 추가로 학습되었지만, 모든 벤치마크에서 DeepSeekMath-Instruct 7B보다 성능이 향상되었습니다.
강화 학습
그룹 상대 정책 최적화
강화 학습(Reinforcement Learning, RL)은 지도 학습 미세 조정(Supervised Fine-Tuning, SFT) 단계 이후 대규모 언어 모델(LLM)의 수학적 추론 능력을 더욱 향상시키는 데 효과적임이 입증되었습니다. 이 섹션에서는 효율적이고 효과적인 RL 알고리즘인 그룹 상대 정책 최적화(Group Relative Policy Optimization, GRPO)를 소개합니다.
PPO에서 GRPO로
근접 정책 최적화(Proximal Policy Optimization, PPO)는 LLM의 RL 미세 조정 단계에서 널리 사용되는 액터-크리틱(actor-critic) RL 알고리즘입니다. 특히, PPO는 다음과 같은 대리 목적 함수를 최대화하여 LLM을 최적화합니다.
\[\mathcal{J}_{PPO}(\theta)=\mathbb{E}{[q\sim P(Q),o\sim\pi_{\theta_{old}}(O|q)]}\frac{1}{|o|}\sum_{t=1}^{|o|}\min\left[\frac{\pi_{\theta}(o_{t}|q,o_{<t})}{\pi_{\theta_{old}}(o_{t}|q,o_{<t})}A_{t},\text{clip}\left(\frac{\pi_{\theta}(o_{t}|q,o_{<t})}{\pi_{\theta_{old}}(o_{t}|q,o_{<t})},1-\varepsilon,1+\varepsilon\right)A_{t}\right]\]여기서 $\pi_{\theta}$와 $\pi_{\theta_{old}}$는 각각 현재와 이전 정책 모델이며, $q, o$는 질문 데이터셋과 이전 정책 $\pi_{\theta_{old}}$에서 샘플링된 질문과 출력입니다. $\varepsilon$은 PPO에서 학습 안정화를 위해 도입된 클리핑 관련 하이퍼파라미터입니다. $A_t$는 일반화된 어드밴티지 추정(Generalized Advantage Estimation, GAE)을 적용하여 계산된 어드밴티지로, 보상 ${r_{\geq t}}$와 학습된 가치 함수 $V_{\psi}$를 기반으로 합니다.
따라서 PPO에서는 정책 모델과 함께 가치 함수를 학습해야 하며, 보상 모델의 과도한 최적화를 완화하기 위해 표준적인 접근 방식은 각 토큰에서 참조 모델로부터의 KL 페널티를 보상에 추가하는 것입니다.
\[r_{t}=r_{\varphi}(q,o_{\leq t})-\beta\log\frac{\pi_{\theta}(o_{t}|q,o_{<t})}{\pi_{ref}(o_{t}|q,o_{<t})}\]여기서 $r_{\varphi}$는 보상 모델, $\pi_{ref}$는 참조 모델(일반적으로 초기 SFT 모델)이며, $\beta$는 KL 페널티의 계수입니다.
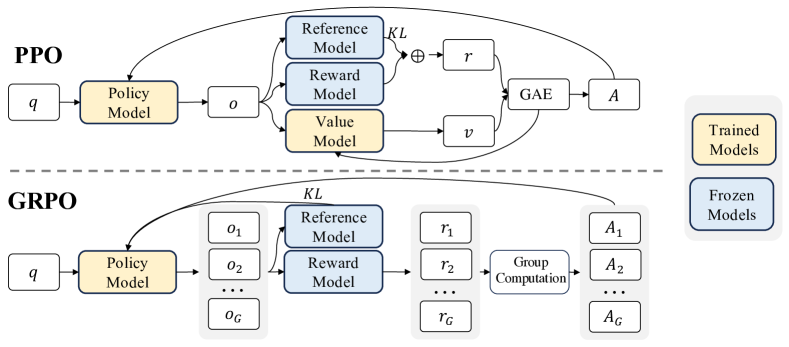
그림 4: PPO와 GRPO의 비교. GRPO는 가치 모델을 사용하지 않고 대신 그룹 점수에서 기준선을 추정하여 학습 리소스를 크게 줄입니다.
PPO에서 사용되는 가치 함수는 일반적으로 정책 모델과 비슷한 크기의 또 다른 모델이므로, 상당한 메모리와 계산 부담을 가져옵니다. 또한 RL 학습 중에 가치 함수는 어드밴티지 계산에서 분산 감소를 위한 기준선으로 취급됩니다. 그러나 LLM 맥락에서는 일반적으로 보상 모델이 마지막 토큰에만 점수를 할당하므로, 각 토큰에서 정확한 가치 함수를 학습하는 것이 복잡해질 수 있습니다.
이를 해결하기 위해, 그림 4에서 볼 수 있듯이, 그룹 상대 정책 최적화(GRPO)를 제안합니다. GRPO는 PPO에서와 같은 추가적인 가치 함수 근사를 필요로 하지 않고, 대신 동일한 질문에 대해 생성된 여러 샘플 출력의 평균 보상을 기준선으로 사용합니다. 구체적으로, 각 질문 $q$에 대해 GRPO는 이전 정책 $\pi_{\theta_{old}}$에서 출력 그룹 ${o_1, o_2, \cdots, o_G}$을 샘플링하고 다음 목적 함수를 최대화하여 정책 모델을 최적화합니다.
\[\begin{split}\mathcal{J}_{GRPO}(\theta)&=\mathbb{E}{[q\sim P(Q),\{o_{i}\}_{i=1}^{G}\sim\pi_{\theta_{old}}(O|q)]}\\ &\frac{1}{G}\sum_{i=1}^{G}\frac{1}{|o_{i}|}\sum_{t=1}^{|o_{i}|}\left\{\min\left[\frac{\pi_{\theta}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q,o_{i,<t})}\hat{A}_{i,t},\text{clip}\left(\frac{\pi_{\theta}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q,o_{i,<t})},1-\varepsilon,1+\varepsilon\right)\hat{A}_{i,t}\right]-\beta\mathbb{D}_{KL}\left[\pi_{\theta}||\pi_{ref}\right]\right\}\end{split}\]여기서 $\varepsilon$과 $\beta$는 하이퍼파라미터이며, $\hat{A}_{i,t}$는 각 그룹 내 출력의 상대적 보상만을 기반으로 계산된 어드밴티지로, 이후 하위 섹션에서 자세히 설명됩니다. GRPO가 어드밴티지를 계산하는 그룹 상대적 방식은 보상 모델이 일반적으로 동일한 질문에 대한 출력 간의 비교 데이터셋에서 학습된다는 점과 잘 일치합니다. 또한 보상에 KL 페널티를 추가하는 대신, GRPO는 학습된 정책과 참조 정책 간의 KL 발산을 손실에 직접 추가하여 정규화하므로, $\hat{A}_{i,t}$의 계산을 복잡하게 만들지 않습니다. 그리고 앞서 사용된 KL 페널티 항과 달리, 다음과 같은 편향되지 않은 추정기를 사용하여 KL 발산을 추정합니다.
\[\mathbb{D}_{KL}\left[\pi_{\theta}||\pi_{ref}\right]=\frac{\pi_{ref}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta}(o_{i,t}|q,o_{i,<t})}-\log\frac{\pi_{ref}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta}(o_{i,t}|q,o_{i,<t})}-1\]이 추정기는 항상 양수임이 보장됩니다.
알고리즘: 반복적 그룹 상대 정책 최적화
입력: 초기 정책 모델 $\pi_{\theta_{\text{init}}}$; 보상 모델 $r_{\varphi}$; 작업 프롬프트 $\mathcal{D}$; 하이퍼파라미터 $\varepsilon$, $\beta$, $\mu$
1: 정책 모델 $\pi_{\theta} \leftarrow \pi_{\theta_{\text{init}}}$
2: for iteration = 1, …, I do
3: 참조 모델 $\pi_{ref} \leftarrow \pi_{\theta}$
4: for step = 1, …, M do
5: $\mathcal{D}$에서 배치 $\mathcal{D}_b$ 샘플링
6: 이전 정책 모델 업데이트 $\pi_{\theta_{old}} \leftarrow \pi_{\theta}$
7: 각 질문 $q \in \mathcal{D}_b$에 대해 $G$ 개의 출력 ${o_i}_{i=1}^{G} \sim \pi_{\theta_{old}}(\cdot \mid q)$ 샘플링
8: $r_{\varphi}$를 실행하여 각 샘플링된 출력 $o_i$에 대한 보상 ${r_i}_{i=1}^{G}$ 계산
9: 그룹 상대 어드밴티지 추정을 통해 $o_i$의 $t$번째 토큰에 대한 $\hat{A}_{i,t}$ 계산
10: for GRPO iteration = 1, …, $\mu$ do
11: GRPO 목적 함수를 최대화하여 정책 모델 $\pi_{\theta}$ 업데이트
12: 재생 메커니즘을 사용한 연속 훈련을 통해 $r_{\varphi}$ 업데이트
출력: $\pi_{\theta}$
결과 감독 RL과 GRPO
형식적으로, 각 질문 $q$에 대해, 이전 정책 모델 $\pi_{\theta_{old}}$에서 출력 그룹 ${o_1, o_2, \cdots, o_G}$이 샘플링됩니다. 그런 다음 보상 모델을 사용하여 출력에 점수를 매기고, 이에 따라 $G$개의 보상 $\mathbf{r}={r_1, r_2, \cdots, r_G}$를 얻습니다. 이후 이러한 보상은 그룹 평균을 빼고 그룹 표준 편차로 나누어 정규화됩니다. 결과 감독은 각 출력 $o_i$의 끝에 정규화된 보상을 제공하고, 출력의 모든 토큰의 어드밴티지 $\hat{A}_{i,t}$를 정규화된 보상으로 설정합니다. 즉, $\hat{A}_{i,t}=\widetilde{r}_{i}=\frac{r_{i}-\text{mean}(\mathbf{r})}{\text{std}(\mathbf{r})}$로 설정하고, 앞의 식에 정의된 목적 함수를 최대화하여 정책을 최적화합니다.
과정 감독 RL과 GRPO
결과 감독은 각 출력의 끝에서만 보상을 제공하므로, 복잡한 수학적 작업에서 정책을 감독하기에 충분하지 않을 수 있습니다. Wang 등의 연구를 따라, 각 추론 단계의 끝에 보상을 제공하는 과정 감독도 탐색합니다. 형식적으로, 질문 $q$와 $G$개의 샘플링된 출력 ${o_1, o_2, \cdots, o_G}$이 주어지면, 과정 보상 모델을 사용하여 출력의 각 단계에 점수를 매기고, 해당하는 보상을 얻습니다.
\[\mathbf{R}=\{\{r_{1}^{index(1)},\cdots,r_{1}^{index(K_{1})}\},\cdots,\{r_{G}^{index(1)},\cdots,r_{G}^{index(K_{G})}\}\}\]여기서 $index(j)$는 $j$번째 단계의 끝 토큰 인덱스이고, $K_i$는 $i$번째 출력의 총 단계 수입니다. 이러한 보상도 평균과 표준 편차로 정규화합니다. $\widetilde{r}_{i}^{index(j)}=\frac{r_{i}^{index(j)}-\text{mean}(\mathbf{R})}{\text{std}(\mathbf{R})}$. 이후, 과정 감독은 각 토큰의 어드밴티지를 다음 단계의 정규화된 보상의 합으로 계산합니다. $\hat{A}_{i,t}=\sum_{index(j)\geq t}\widetilde{r}_{i}^{index(j)}$, 그리고 앞의 식에 정의된 목적 함수를 최대화하여 정책을 최적화합니다.
반복적 RL과 GRPO
강화 학습 훈련 과정이 진행됨에 따라, 이전 보상 모델이 현재 정책 모델을 감독하기에 충분하지 않을 수 있습니다. 따라서 GRPO와 함께 반복적 RL도 탐색합니다. 알고리즘에서 볼 수 있듯이, 반복적 GRPO에서는 정책 모델의 샘플링 결과를 기반으로 보상 모델을 위한 새로운 학습 세트를 생성하고, 역사적 데이터의 10%를 통합하는 재생 메커니즘을 사용하여 이전 보상 모델을 지속적으로 학습시킵니다. 그런 다음 참조 모델을 정책 모델로 설정하고, 새로운 보상 모델로 정책 모델을 지속적으로 학습시킵니다.
DeepSeekMath-RL의 학습 및 평가
DeepSeekMath-Instruct 7B를 기반으로 RL을 수행합니다. RL의 학습 데이터는 SFT 데이터에서 GSM8K 및 MATH와 관련된 체인 오브 소트 형식의 질문으로, 약 144K개의 질문으로 구성됩니다. RL 단계에서 데이터가 부족한 벤치마크에 대한 RL의 영향을 조사하기 위해 다른 SFT 질문은 제외합니다. Wang 등의 연구를 따라 보상 모델의 학습 세트를 구성합니다. 2e-5의 학습률로 DeepSeekMath-Base 7B를 기반으로 초기 보상 모델을 학습합니다. GRPO의 경우, 정책 모델의 학습률을 1e-6으로 설정합니다. KL 계수는 0.04입니다. 각 질문에 대해 64개의 출력을 샘플링합니다. 최대 길이는 1024로 설정되고, 학습 배치 크기는 1024입니다. 정책 모델은 각 탐색 단계 이후에 단 한 번의 업데이트만 수행합니다.
DeepSeekMath-RL 7B를 DeepSeekMath-Instruct 7B를 따라 벤치마크에서 평가합니다. DeepSeekMath-RL 7B의 경우, 체인 오브 소트 추론을 사용한 GSM8K와 MATH는 도메인 내 작업으로 간주될 수 있으며, 다른 모든 벤치마크는 도메인 외 작업으로 간주될 수 있습니다. 표 5는 영어와 중국어 벤치마크에서 체인 오브 소트와 도구 통합 추론을 모두 사용한 오픈소스 및 비공개 소스 모델의 성능을 보여줍니다. 다음과 같은 결과를 발견했습니다.
1) DeepSeekMath-RL 7B는 체인 오브 소트 추론을 사용하여 GSM8K와 MATH에서 각각 88.2%와 51.7%의 정확도를 달성합니다. 이 성능은 7B에서 70B 범위의 모든 오픈소스 모델뿐만 아니라 대부분의 비공개 소스 모델을 능가합니다.
2) 중요한 점은, DeepSeekMath-RL 7B는 DeepSeekMath-Instruct 7B에서 시작하여 GSM8K와 MATH의 체인 오브 소트 형식 명령어 튜닝 데이터에 대해서만 학습되었습니다. 학습 데이터의 제한된 범위에도 불구하고, 모든 평가 지표에서 DeepSeekMath-Instruct 7B를 능가하여 강화 학습의 효과를 보여줍니다.
논의
이 섹션에서는 사전 학습과 강화 학습 실험에서 얻은 연구 결과를 공유합니다.
사전 학습에서 얻은 교훈
먼저 사전 학습 과정에서의 경험을 공유하겠습니다. 특별히 언급하지 않는 한, 앞서 설명된 학습 설정을 따릅니다. 이 섹션에서 DeepSeekMath 코퍼스를 언급할 때는 데이터 수집 과정의 두 번째 반복에서 얻은 89B 토큰 데이터셋을 사용했음을 참고하시기 바랍니다.
코드 학습이 수학적 추론에 도움이 됩니다
코드 학습이 추론 능력을 향상시킨다는 가설은 널리 알려져 있지만 아직 검증되지 않았습니다. 이에 대해 수학적 영역에서 부분적인 답변을 제시하고자 합니다. 코드 학습은 도구 사용 여부와 관계없이 모델의 수학적 추론 능력을 향상시킵니다.
코드 학습이 수학적 추론에 미치는 영향을 연구하기 위해 다음과 같은 2단계 학습 및 1단계 학습 설정으로 실험했습니다.
2단계 학습
- 코드 학습 400B 토큰 → 수학 학습 150B 토큰: DeepSeek-LLM 1.3B를 400B 코드 토큰으로 학습한 후 150B 수학 토큰으로 학습했습니다.
- 일반 학습 400B 토큰 → 수학 학습 150B 토큰: 대조 실험으로, 첫 단계에서 코드 토큰 대신 일반 토큰(DeepSeek-AI에서 만든 대규모 일반 코퍼스에서 샘플링)을 사용하여 수학적 추론 향상에 있어 코드 토큰의 이점을 조사했습니다.
1단계 학습
- 수학 학습 150B 토큰: DeepSeek-LLM 1.3B를 150B 수학 토큰으로 학습했습니다.
- 400B 코드 토큰과 150B 수학 토큰의 혼합 학습: 코드 학습 후 수학 학습은 코딩 성능을 저하시킵니다. 1단계 학습에서 코드 토큰과 수학 토큰을 혼합했을 때도 수학적 추론을 향상시키고 파국적 망각 문제를 완화할 수 있는지 조사했습니다.
결과
코드 학습은 2단계 학습과 1단계 학습 설정 모두에서 프로그램 지원 수학적 추론에 도움이 됩니다. 2단계 학습 설정에서 코드 학습만으로도 Python을 사용하여 GSM8K와 MATH 문제를 해결하는 능력이 크게 향상됩니다. 두 번째 단계의 수학 학습은 추가적인 개선을 가져옵니다. 흥미롭게도, 1단계 학습 설정에서 코드 토큰과 수학 토큰을 혼합하면 2단계 학습에서 발생하는 파국적 망각 문제를 효과적으로 완화하고, 코딩과 프로그램 지원 수학적 추론의 시너지 효과를 가져옵니다.
코드 학습은 도구 사용 없이도 수학적 추론 능력을 향상시킵니다. 2단계 학습 설정에서 초기 코드 학습 단계만으로도 적당한 향상이 이루어집니다. 또한 이후 수학 학습의 효율성을 높여 결국 최고의 성능을 이끌어냅니다. 그러나 1단계 학습에서 코드 토큰과 수학 토큰을 결합하면 도구 사용 없는 수학적 추론 능력이 저하됩니다. 이는 DeepSeek-LLM 1.3B가 규모의 제한으로 인해 코드와 수학 데이터를 동시에 완전히 흡수할 수 있는 용량이 부족하기 때문일 수 있습니다.
arXiv 논문은 수학적 추론 향상에 효과적이지 않은 것으로 보입니다
arXiv 논문은 일반적으로 수학 사전 학습 데이터의 구성 요소로 포함됩니다(Lewkowycz 등, 2022a; Polu와 Sutskever, 2020; Azerbayev 등, 2023; Wang 등, 2023c). 그러나 수학적 추론에 미치는 영향에 대한 자세한 분석은 광범위하게 수행되지 않았습니다. 직관과는 반대로, 실험 결과에 따르면 arXiv 논문은 수학적 추론 향상에 효과적이지 않은 것으로 보입니다.
DeepSeek-LLM 1.3B와 DeepSeek-Coder-Base-v1.5 7B(Guo 등, 2024)를 포함한 다양한 크기의 모델로 실험했으며, 다양한 처리 파이프라인을 거친 arXiv 코퍼스를 사용했습니다.
- MathPile(Wang 등, 2023c): 정리 및 필터링 휴리스틱 규칙으로 개발된 8.9B 토큰 코퍼스로, 85% 이상이 과학적 arXiv 논문입니다.
- ArXiv-RedPajama(Computer, 2023): 서문, 주석, 매크로, 참고 문헌이 제거된 arXiv LaTeX 파일 전체로, 총 28.0B 토큰입니다.
실험에서는 DeepSeek-LLM 1.3B를 150B 토큰, DeepSeek-Coder-Base-v1.5 7B를 40B 토큰으로 각 arXiv 코퍼스에 대해 별도로 학습시켰습니다.
arXiv 논문은 수학적 추론 향상에 효과적이지 않은 것으로 보입니다. arXiv 전용 코퍼스로 학습했을 때, 두 모델 모두 이 연구에서 사용된 다양한 수학적 벤치마크에서 주목할 만한 개선을 보이지 않거나 오히려 성능이 저하되었습니다. 이러한 벤치마크에는 GSM8K와 MATH와 같은 정량적 추론 데이터셋, MMLU-STEM과 같은 객관식 문제, miniF2F와 같은 형식적 수학이 포함됩니다.
그러나 이 결론에는 한계가 있으며 주의해서 받아들여야 합니다. 아직 연구하지 않은 부분은 다음과 같습니다.
- 이 연구에 포함되지 않은 정리의 비형식화와 같은 특정 수학 관련 작업에 대한 arXiv 토큰의 영향
- 다른 유형의 데이터와 결합했을 때 arXiv 토큰의 효과
- 더 큰 모델 규모에서 arXiv 논문의 이점이 나타날 수 있는지 여부
따라서 추가적인 탐색이 필요하며, 이는 향후 연구 과제로 남겨둡니다.
강화 학습의 통찰
통합 패러다임을 향하여
이 섹션에서는 SFT(Supervised Fine-Tuning), RFT(Rejection Sampling Fine-Tuning), DPO(Direct Preference Optimization), PPO(Proximal Policy Optimization), GRPO(Group Relative Policy Optimization)와 같은 다양한 학습 방법을 분석하기 위한 통합 패러다임을 제공하고, 이 통합 패러다임의 요소를 탐색하는 실험을 추가로 수행합니다.
일반적으로 학습 방법의 매개변수 $\theta$에 대한 그래디언트는 다음과 같이 작성할 수 있습니다.
\[\nabla_\theta \mathcal{J}_\mathcal{A}(\theta) = \mathbb{E}_{(q, o) \sim \mathcal{D}}[\frac{1}{|o|}\sum_{t=1}^{|o|} GC_\mathcal{A}(q, o, t, \pi_{rf})\nabla_\theta \log \pi_\theta(o_t|q, o_{<t})].\]여기에는 세 가지 핵심 구성 요소가 있습니다. 1) 데이터 소스 $\mathcal{D}$: 학습 데이터를 결정합니다. 2) 보상 함수 $\pi_{rf}$: 학습 보상 신호의 소스입니다. 3) 알고리즘 $\mathcal{A}$: 학습 데이터와 보상 신호를 처리하여 데이터에 대한 페널티나 강화의 크기를 결정하는 그래디언트 계수 $GC$를 계산합니다.
다음과 같은 대표적인 방법들을 이 통합 패러다임을 기반으로 분석합니다.
- 지도 미세 조정(SFT): SFT는 인간이 선택한 SFT 데이터에 대해 사전 학습된 모델을 미세 조정합니다.
- 거부 샘플링 미세 조정(RFT): RFT는 SFT 질문을 기반으로 SFT 모델에서 샘플링된 필터링된 출력에 대해 SFT 모델을 추가로 미세 조정합니다. RFT는 답변의 정확성을 기준으로 출력을 필터링합니다.
- 직접 선호도 최적화(DPO): DPO는 SFT 모델에서 샘플링된 증강 출력에 대해 쌍별 DPO 손실을 사용하여 SFT 모델을 추가로 개선합니다.
- 온라인 거부 샘플링 미세 조정(Online RFT): RFT와 달리, Online RFT는 SFT 모델을 사용하여 정책 모델을 초기화하고 실시간 정책 모델에서 샘플링된 증강 출력으로 미세 조정합니다.
- PPO/GRPO: PPO/GRPO는 SFT 모델을 사용하여 정책 모델을 초기화하고 실시간 정책 모델에서 샘플링된 출력으로 강화합니다.
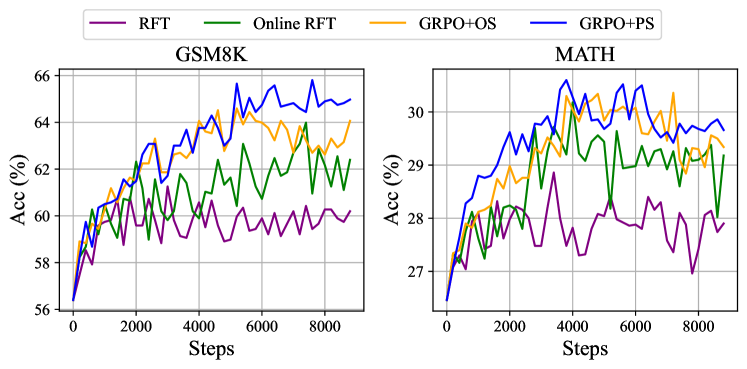
그림 5: 다양한 방법으로 추가 학습된 DeepSeekMath-Instruct 1.3B 모델의 두 벤치마크에서의 성능.
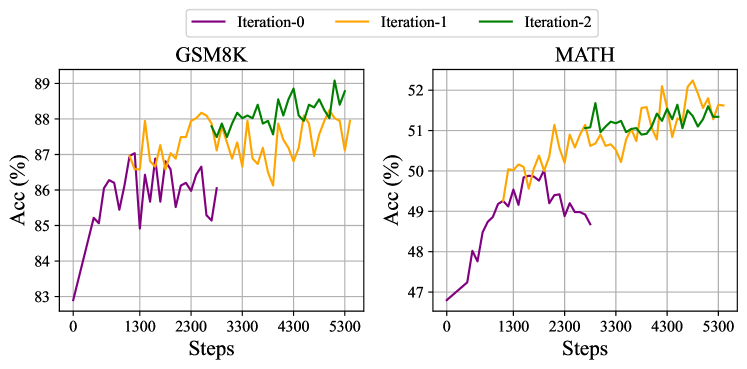
그림 6: DeepSeekMath-Instruct 7B를 사용한 반복적 강화 학습의 두 벤치마크에서의 성능.
데이터 소스에 대한 관찰
데이터 소스를 온라인 샘플링과 오프라인 샘플링의 두 가지 범주로 나눕니다. 온라인 샘플링은 실시간 학습 정책 모델의 탐색 결과에서 학습 데이터를 가져오는 것을 의미하고, 오프라인 샘플링은 초기 SFT 모델의 샘플링 결과에서 학습 데이터를 가져오는 것을 의미합니다. RFT와 DPO는 오프라인 스타일을 따르고, Online RFT와 GRPO는 온라인 스타일을 따릅니다.
그림 5에서 볼 수 있듯이, Online RFT는 두 벤치마크에서 RFT보다 크게 성능이 우수합니다. 구체적으로, Online RFT는 학습 초기 단계에서는 RFT와 비슷하지만 후반부에는 절대적인 우위를 보여 온라인 학습의 우수성을 입증합니다. 이는 직관적으로 이해할 수 있는데, 초기 단계에서는 액터와 SFT 모델이 매우 유사하여 샘플링된 데이터에 작은 차이만 나타나지만, 후반부에서는 액터에서 샘플링된 데이터가 더 큰 차이를 보이므로 실시간 데이터 샘플링이 더 큰 이점을 제공합니다.
그래디언트 계수에 대한 관찰
알고리즘은 보상 신호를 그래디언트 계수로 처리하여 모델 매개변수를 업데이트합니다. 실험에서는 보상 함수를 ‘규칙’과 ‘모델’로 나눕니다. 규칙은 답변의 정확성을 기준으로 응답의 품질을 판단하는 것을 의미하고, 모델은 각 응답에 점수를 매기는 보상 모델을 학습하는 것을 의미합니다. 보상 모델의 학습 데이터는 규칙 판단을 기반으로 합니다.
부록의 방정식은 GRPO와 Online RFT의 핵심적인 차이점을 강조합니다. GRPO는 보상 모델이 제공하는 보상 값에 따라 그래디언트 계수를 고유하게 조정합니다. 이를 통해 응답의 다양한 크기에 따라 차별적인 강화와 페널티를 적용할 수 있습니다. 반면 Online RFT는 이러한 기능이 없어, 잘못된 응답에 페널티를 주지 않고 정답이 있는 모든 응답을 동일한 강도로 균일하게 강화합니다.
그림 5에서 볼 수 있듯이, GRPO는 Online RFT를 능가하여 긍정적 및 부정적 그래디언트 계수를 변경하는 효율성을 강조합니다. 또한 GRPO+PS는 GRPO+OS보다 우수한 성능을 보여 세분화된 단계별 그래디언트 계수를 사용하는 이점을 나타냅니다.
또한 반복적 RL을 탐색하며, 실험에서는 두 라운드의 반복을 수행합니다. 그림 6에서 볼 수 있듯이, 반복적 RL은 특히 첫 번째 반복에서 성능을 크게 향상시키는 것을 알 수 있습니다.
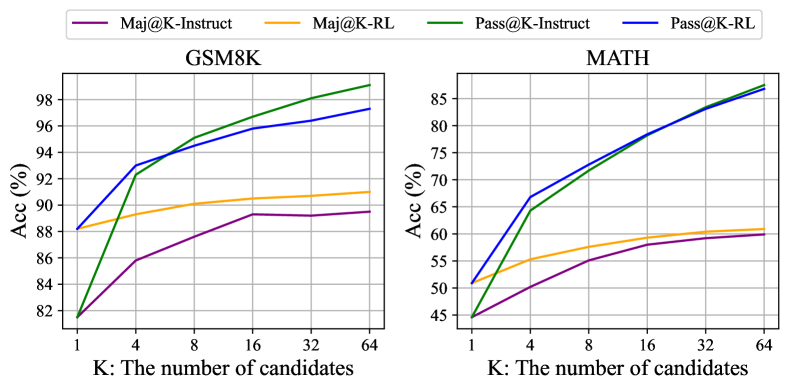
그림 7: GSM8K와 MATH에서 SFT와 RL DeepSeekMath 7B의 Maj@K와 Pass@K(온도 0.7). RL은 Pass@K가 아닌 Maj@K를 향상시키는 것으로 나타났습니다.
RL이 효과적인 이유는 무엇인가?
이 논문에서는 명령어 튜닝 데이터의 하위 집합을 기반으로 강화 학습을 수행하며, 이는 명령어 튜닝 모델의 성능을 크게 향상시킵니다. 강화 학습이 효과적인 이유를 더 설명하기 위해, 두 벤치마크에서 Instruct 및 RL 모델의 Pass@K와 Maj@K 정확도를 평가합니다. 그림 7에서 볼 수 있듯이, RL은 Pass@K가 아닌 Maj@K의 성능을 향상시킵니다. 이러한 결과는 RL이 출력 분포를 더 견고하게 만들어 모델의 전반적인 성능을 향상시키는 것으로 보입니다. 다시 말해, 개선은 기본적인 능력의 향상보다는 TopK에서 올바른 응답을 증가시키는 데 기인하는 것으로 보입니다.
유사하게, Wang 등(2023a)은 SFT 모델 내에서 추론 작업의 불일치 문제를 식별하고, SFT 모델의 추론 성능이 일련의 선호도 정렬 전략(Yuan 등, 2023b; Song 등, 2023; Wang 등, 2023a)을 통해 개선될 수 있음을 보여주었습니다.
더 효과적인 RL을 달성하는 방법
수학적 추론 작업에서 RL이 매우 효과적으로 작동함을 보여주었습니다. 또한 다양한 대표적인 학습 방법을 이해하기 위한 통합 패러다임을 제공했습니다. 이 패러다임 내에서 모든 방법은 직접적이거나 단순화된 RL 기술로 개념화됩니다. 앞선 방정식에 요약된 바와 같이, 데이터 소스, 알고리즘, 보상 함수라는 세 가지 핵심 구성 요소가 있습니다. 이 세 가지 구성 요소에 대한 몇 가지 잠재적인 미래 방향을 제시합니다.
데이터 소스
데이터 소스는 모든 학습 방법의 원재료입니다. RL의 맥락에서는 데이터 소스를 정책 모델에서 샘플링된 출력이 있는 레이블이 없는 질문으로 특별히 지칭합니다. 이 논문에서는 명령어 튜닝 단계의 질문만 사용하고 단순한 핵 샘플링을 사용하여 출력을 샘플링합니다. 이것이 RL 파이프라인이 Maj@K 성능만 향상시키는 잠재적인 이유일 수 있습니다. 향후에는 분포 외 질문 프롬프트에 대한 RL 파이프라인을 탐색하고, 트리 검색 방법(Yao 등, 2023)과 같은 고급 샘플링(디코딩) 전략과 결합할 계획입니다. 또한 정책 모델의 탐색 효율성을 결정하는 효율적인 추론 기술(Xia 등, 2023; Leviathan 등, 2023; Kwon 등, 2023; Xia 등, 2024)도 매우 중요한 역할을 합니다.
알고리즘
알고리즘은 데이터와 보상 신호를 그래디언트 계수로 처리하여 모델 매개변수를 업데이트합니다. 앞선 방정식을 기반으로, 어느 정도까지 모든 방법은 특정 토큰의 조건부 확률을 증가시키거나 감소시키기 위해 보상 함수의 신호를 완전히 신뢰합니다. 그러나 특히 극도로 복잡한 작업에서는 보상 신호가 항상 신뢰할 수 있다고 보장할 수 없습니다. 예를 들어, 잘 훈련된 주석자들이 신중하게 주석을 단 PRM800K 데이터셋(Lightman 등, 2023)조차도 약 20%의 잘못된 주석을 포함하고 있습니다. 이를 위해 노이즈가 있는 보상 신호에 강건한 강화 학습 알고리즘을 탐색할 계획입니다. 이러한 WEAK-TO-STRONG(Burns 등, 2023) 정렬 방법이 학습 알고리즘에 근본적인 변화를 가져올 것이라고 믿습니다.
보상 함수
보상 함수는 학습 신호의 소스입니다. RL에서 보상 함수는 일반적으로 신경망 보상 모델입니다. 보상 모델에 대해 세 가지 중요한 방향이 있다고 생각합니다. 1) 보상 모델의 일반화 능력을 향상시키는 방법. 보상 모델은 분포 외 질문과 고급 디코딩 출력을 효과적으로 처리할 수 있어야 합니다. 그렇지 않으면 강화 학습은 LLM의 기본 능력을 향상시키기보다는 단순히 분포를 안정화시킬 수 있습니다. 2) 보상 모델의 불확실성을 반영하는 방법. 불확실성은 약한 보상 모델과 약-강 학습 알고리즘 사이의 연결 다리 역할을 할 수 있습니다. 3) 추론 과정에 대한 세분화된 학습 신호를 제공할 수 있는 고품질 프로세스 보상 모델을 효율적으로 구축하는 방법(Lightman 등, 2023; Wang 등, 2023b).
결론, 한계점 및 향후 연구 방향
본 논문에서는 DeepSeekMath를 소개했습니다. 이 모델은 경쟁 수준의 MATH 벤치마크에서 모든 오픈소스 모델을 능가하는 성능을 보이며, 비공개 모델들의 성능에 근접합니다. DeepSeekMath는 DeepSeek-Coder-v1.5 7B로 초기화되어 500B 토큰에 대해 지속적인 학습을 진행했으며, 학습 데이터의 상당 부분은 Common Crawl에서 추출한 120B 수학 토큰으로 구성되었습니다.
광범위한 실험 결과, 웹 페이지가 고품질 수학 데이터의 중요한 잠재력을 가지고 있는 반면, arXiv는 예상만큼 유익하지 않은 것으로 나타났습니다. 또한 근접 정책 최적화(PPO)의 변형인 그룹 상대 정책 최적화(GRPO)를 도입했는데, 이는 메모리 사용량을 줄이면서도 수학적 추론 능력을 크게 향상시킬 수 있습니다. 실험 결과에 따르면, DeepSeekMath-Instruct 7B가 벤치마크에서 이미 높은 점수를 달성했음에도 불구하고 GRPO는 여전히 효과적인 것으로 나타났습니다. 또한 일련의 방법론을 이해하기 위한 통합 패러다임을 제공하고, 더 효과적인 강화 학습을 위한 여러 잠재적 방향을 요약했습니다.
DeepSeekMath가 정량적 추론 벤치마크에서 인상적인 점수를 달성했지만, 기하학과 정리 증명 분야에서는 비공개 모델들보다 상대적으로 약한 성능을 보입니다. 예를 들어, 저자들의 예비 실험에서 모델은 삼각형과 타원에 관련된 문제를 처리하는 데 어려움을 겪었는데, 이는 사전 학습과 미세 조정에서의 데이터 선택 편향을 나타낼 수 있습니다. 또한 모델 규모의 제한으로 인해 DeepSeekMath는 퓨 샷 능력에서 GPT-4보다 성능이 떨어집니다. GPT-4는 퓨 샷 입력으로 성능을 향상시킬 수 있는 반면, DeepSeekMath는 제로 샷과 퓨 샷 평가에서 유사한 성능을 보입니다.
향후 연구에서는 더 고품질의 사전 학습 코퍼스를 구축하기 위한 데이터 선택 파이프라인을 개선할 계획입니다. 또한 대규모 언어 모델의 더 효과적인 강화 학습을 위해 해당 절에서 제시한 잠재적 방향을 탐색할 예정입니다.
이 연구는 수학적 추론 능력을 갖춘 오픈소스 언어 모델 개발에 중요한 진전을 이루었으며, 특히 웹 데이터의 효과적인 활용과 효율적인 강화 학습 방법론을 통해 이를 달성했습니다. DeepSeekMath의 성공은 대규모 모델 크기만으로는 수학적 추론 능력을 향상시키기에 충분하지 않으며, 고품질 데이터와 효과적인 학습 방법론의 조합이 중요하다는 것을 보여줍니다. 이러한 접근 방식은 향후 다양한 도메인에서의 언어 모델 개발에도 적용될 수 있을 것입니다.
DeepSeekMath의 한계점은 특정 수학 분야에서의 약점과 모델 규모로 인한 제약을 명확히 보여주지만, 동시에 이러한 한계를 극복하기 위한 구체적인 연구 방향을 제시합니다. 특히 데이터 선택 파이프라인의 개선과 강화 학습 방법론의 발전은 향후 수학적 추론 능력을 더욱 향상시키는 데 중요한 역할을 할 것으로 기대됩니다.
부록 A
A.1 강화 학습 분석
여기서는 다양한 방법론(SFT, RFT, Online RFT, DPO, PPO, GRPO)에 걸쳐 데이터 소스와 그래디언트 계수(알고리즘 및 보상 함수)의 상세한 유도 과정을 제공합니다.
A.1.1 지도 미세 조정(Supervised Fine-tuning)
지도 미세 조정의 목적은 다음 목적 함수를 최대화하는 것입니다.
\[\mathcal{J}_{SFT}(\theta) = \mathbb{E}_{[q, o \sim P_{sft}(Q, O)]}\left(\frac{1}{|o|}\sum_{t=1}^{|o|} \log \pi_\theta(o_t|q, o_{<t})\right).\]$\mathcal{J}_{SFT}(\theta)$의 그래디언트는 다음과 같습니다.
\[\nabla_{\theta}\mathcal{J}_{SFT} = \mathbb{E}_{[q, o \sim P_{sft}(Q, O)]}\left(\frac{1}{|o|}\sum_{t=1}^{|o|} \nabla_{\theta}\log\pi_{\theta}(o_{t}|q,o_{<t})\right).\]데이터 소스: SFT에 사용되는 데이터셋입니다. 보상 함수: 인간의 선택으로 간주될 수 있습니다. 그래디언트 계수: 항상 1로 설정됩니다.
A.1.2 거부 샘플링 미세 조정(Rejection Sampling Fine-tuning)
거부 샘플링 미세 조정은 먼저 지도 미세 조정된 LLM에서 각 질문에 대해 여러 출력을 샘플링한 다음, 정답이 있는 샘플링된 출력에 대해 LLM을 학습시킵니다. 형식적으로, RFT의 목적은 다음 목적 함수를 최대화하는 것입니다.
\[\mathcal{J}_{RFT}(\theta) = \mathbb{E}_{[q \sim P_{sft}(Q), o \sim \pi_{sft}(O|q)]}\left(\frac{1}{|o|}\sum_{t=1}^{|o|}\mathbb{I}(o)\log\pi_{\theta}(o_{t}|q,o_{<t})\right).\]$\mathcal{J}_{RFT}(\theta)$의 그래디언트는 다음과 같습니다.
\[\nabla_{\theta}\mathcal{J}_{RFT}(\theta) = \mathbb{E}_{[q \sim P_{sft}(Q), o \sim \pi_{sft}(O|q)]}\left(\frac{1}{|o|}\sum_{t=1}^{|o|}\mathbb{I}(o)\nabla_{\theta}\log\pi_{\theta}(o_{t}|q,o_{<t})\right).\]데이터 소스: SFT 데이터셋의 질문과 SFT 모델에서 샘플링된 출력입니다. 보상 함수: 규칙(답변이 맞는지 여부)입니다. 그래디언트 계수:
\[GC_{RFT}(q,o,t) = \mathbb{I}(o) = \left\{\begin{aligned} 1&&{\rm if \, the \, answer \, in \, output \, o \, is \, correct}\\ 0&&{\rm if \, the \, answer \, in \, output \, o \, is \, incorrect}\\ \end{aligned}\right.\]A.1.3 온라인 거부 샘플링 미세 조정(Online Rejection Sampling Fine-tuning)
RFT와 Online RFT의 유일한 차이점은 Online RFT가 SFT 모델 $\pi_{\theta_{sft}}$에서 샘플링하는 대신 실시간 정책 모델 $\pi_{\theta}$에서 출력을 샘플링한다는 것입니다. 따라서 Online RFT의 그래디언트는 다음과 같습니다.
\[\nabla_{\theta}\mathcal{J}_{OnRFT}(\theta) = \mathbb{E}_{[q \sim P_{sft}(Q), o \sim \pi_{\theta}(O|q)]}\left(\frac{1}{|o|}\sum_{t=1}^{|o|}\mathbb{I}(o)\nabla_{\theta}\log\pi_{\theta}(o_{t}|q,o_{<t})\right).\]A.1.4 직접 선호도 최적화(Direct Preference Optimization, DPO)
DPO의 목적 함수는 다음과 같습니다.
\[\mathcal{J}_{DPO}(\theta) = \mathbb{E}_{[q \sim P_{sft}(Q), o^+, o^- \sim \pi_{sft}(O|q)]}\log\sigma\left(\beta\frac{1}{|o^+|}\sum_{t=1}^{|o^+|}\log\frac{\pi_{\theta}(o^+_{t}|q,o^+_{<t})}{\pi_{\text{ref}}(o^+_{t}|q,o^+_{<t})}-\beta\frac{1}{|o^-|}\sum_{t=1}^{|o^-|}\log\frac{\pi_{\theta}(o^-_{<t}|q,o^-_{<t})}{\pi_{\text{ref}}(o^-_{<t}|q,o^-_{<t})}\right)\]$\mathcal{J}_{DPO}(\theta)$의 그래디언트는 다음과 같습니다.
\[\begin{split} \nabla_{\theta}\mathcal{J}_{DPO}(\theta) = \mathbb{E}_{[q \sim P_{sft}(Q), o^+, o^- \sim \pi_{sft}(O|q)]}&\left(\frac{1}{|o^+|}\sum_{t=1}^{|o^+|}GC_{DPO}(q,o,t)\nabla_{\theta}\log\pi_{\theta}(o^+_{t}|q,o^+_{<t})\right.\\ -&\left.\frac{1}{|o^-|}\sum_{t=1}^{|o^-|}GC_{DPO}(q,o,t)\nabla_{\theta}\log\pi_{\theta}(o^-_{t}|q,o^-_{<t})\right)\end{split}\]데이터 소스: SFT 데이터셋의 질문과 SFT 모델에서 샘플링된 출력입니다. 보상 함수: 일반 도메인에서의 인간 선호도(수학적 작업에서는 ‘규칙’일 수 있음)입니다. 그래디언트 계수:
\[GC_{DPO}(q,o,t) = \sigma\left(\beta\log\frac{\pi_{\theta}(o^-_{t}|q,o^-_{<t})}{\pi_{\text{ref}}(o^-_{t}|q,o^-_{<t})}-\beta\log\frac{\pi_{\theta}(o^+_{t}|q,o^+_{<t})}{\pi_{\text{ref}}(o^+_{t}|q,o^+_{<t})}\right)\]A.1.5 근접 정책 최적화(Proximal Policy Optimization, PPO)
PPO의 목적 함수는 다음과 같습니다.
\[\mathcal{J}_{PPO}(\theta) = \mathbb{E}_{[q \sim P_{sft}(Q), o \sim \pi_{\theta_{old}}(O|q)]}\left[\frac{1}{|o|}\sum_{t=1}^{|o|}\min\left[\frac{\pi_{\theta}(o_t|q,o_{<t})}{\pi_{\theta_{old}}(o_t|q,o_{<t})}A_t, \text{clip}\left(\frac{\pi_{\theta}(o_t|q,o_{<t})}{\pi_{\theta_{old}}(o_t|q,o_{<t})}, 1-\varepsilon, 1+\varepsilon\right)A_t\right]\right].\]분석을 단순화하기 위해, 모델이 각 탐색 단계 이후에 단 한 번의 업데이트만 수행하여 $\pi_{\theta_{old}} = \pi_{\theta}$가 되도록 가정합니다. 이 경우 $\min$과 $\text{clip}$ 연산을 제거할 수 있습니다.
\[\mathcal{J}_{PPO}(\theta) = \mathbb{E}_{[q \sim P_{sft}(Q), o \sim \pi_{\theta_{old}}(O|q)]}\frac{1}{|o|}\sum_{t=1}^{|o|}\frac{\pi_{\theta}(o_t|q,o_{<t})}{\pi_{\theta_{old}}(o_t|q,o_{<t})}A_t.\]$\mathcal{J}_{PPO}(\theta)$의 그래디언트는 다음과 같습니다.
\[\begin{split} \nabla_{\theta}\mathcal{J}_{PPO}(\theta) = \mathbb{E}_{[q \sim P_{sft}(Q), o \sim \pi_{\theta_{old}}(O|q)]}\frac{1}{|o|}\sum_{t=1}^{|o|}A_t\nabla_{\theta}\log\pi_{\theta}(o_t|q,o_{<t})\end{split}\]데이터 소스: 정책 모델에서 샘플링된 출력이 있는 SFT 데이터셋의 질문입니다. 보상 함수: 보상 모델입니다. 그래디언트 계수:
\[GC_{PPO}(q,o,t,\pi_{\theta_{rm}}) = A_t,\]여기서 $A_t$는 어드밴티지로, 보상 ${r_{\geq t}}$와 학습된 가치 함수 $V_{\psi}$를 기반으로 일반화된 어드밴티지 추정(GAE)(Schulman 등, 2015)을 적용하여 계산됩니다.
A.1.6 그룹 상대 정책 최적화(Group Relative Policy Optimization, GRPO)
GRPO의 목적 함수는 다음과 같습니다(단순화된 분석을 위해 $\pi_{\theta_{old}} = \pi_{\theta}$ 가정):
\[\begin{split}\mathcal{J}_{GRPO}(\theta)&=\mathbb{E}{[q\sim P_{sft}(Q),\{o_{i}\}_{i=1}^{G}\sim\pi_{\theta_{old}}(O|q)]}\\ &\frac{1}{G}\sum_{i=1}^{G}\frac{1}{|o_{i}|}\sum_{t=1}^{|o_{i}|}\left[\frac{\pi_{\theta}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{old}}(o_{i,t}|q,o_{i,<t})}\hat{A}_{i,t}-\beta\left(\frac{\pi_{ref}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta}(o_{i,t}|q,o_{i,<t})}-\log\frac{\pi_{ref}(o_{i,t}|q,o_{i,<t})}{\pi_{\theta}(o_{i,t}|q,o_{i,<t})}-1\right)\right].\end{split}\]$\mathcal{J}_{GRPO}(\theta)$의 그래디언트는 다음과 같습니다.
\[\begin{split} \nabla_{\theta}\mathcal{J}_{GRPO}(\theta)&=\mathbb{E}{[q\sim P_{sft}(Q),\{o_{i}\}_{i=1}^{G}\sim\pi_{\theta_{old}}(O|q)]}\\ &\frac{1}{G}\sum_{i=1}^{G}\frac{1}{|o_{i}|}\sum_{t=1}^{|o_{i}|}\left[\hat{A}_{i,t}+\beta\left(\frac{\pi_{ref}(o_{i,t}|o_{i,<t})}{\pi_{\theta}(o_{i,t}|o_{i,<t})}-1\right)\right]\nabla_{\theta}\log\pi_{\theta}(o_{i,t}|q,o_{i,<t}).\end{split}\]데이터 소스: 정책 모델에서 샘플링된 출력이 있는 SFT 데이터셋의 질문입니다. 보상 함수: 보상 모델입니다. 그래디언트 계수:
\[GC_{GRPO}(q,o,t,\pi_{\theta_{rm}}) = \hat{A}_{i,t}+\beta\left(\frac{\pi_{ref}(o_{i,t}|o_{i,<t})}{\pi_{\theta}(o_{i,t}|o_{i,<t})}-1\right),\]여기서 $\hat{A}_{i,t}$는 그룹 보상 점수를 기반으로 계산됩니다.
References
Subscribe via RSS
